题目内容
已知函数f(x)=
ex(a>0),g(x)=[a(x-1)]ex-f(x).
(1)当a=1时?x∈(0,+∞)都有g(x)≥1成立,求b的最大值;
(2)当?x>1,使g(x)+g′(x)=0成立,求
的取值范围.
| ax+b |
| x |
(1)当a=1时?x∈(0,+∞)都有g(x)≥1成立,求b的最大值;
(2)当?x>1,使g(x)+g′(x)=0成立,求
| b |
| a |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)利用分离变量法,由已知变量的取值范围求出参数的取值范围,通过构造新的函数,等价转化;
(2)存在x>1,使g(x)+g′(x)=0成立,等价于存在x>1,2ax3-3ax2-2bx+b=0成立,设u(x)=
(x>1),求出u(x)的最小值即可.
(2)存在x>1,使g(x)+g′(x)=0成立,等价于存在x>1,2ax3-3ax2-2bx+b=0成立,设u(x)=
| 2x3-3x2 |
| 2x-1 |
解答:
解:(1)当a=1时,g(x)=(x-
-2)ex,
∵g(x)≥1在x∈(0,+∞)上恒成立,
∴b≤x2-2x-
在x∈(0,+∞)上恒成立.
记h(x)=x2-2x-
,(x>0),则h′(x)=
,
当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数;
∴h(x)min=h(1)=-1-e-1,
∴b的最大值为-1-e-1.
②∵g(x)=(ax-
-2a)ex,
∴g′(x)=(
+ax-
-a)ex,
∴由g(x)+g′(x)=0,整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g(x)+g′(x)=0成立,
等价于存在x>1,2ax3-3ax2-2bx+b=0成立,
∵a>0,∴
=
,
设u(x)=
(x>1),则u′(x)=
,
∵x>1,∴u′(x)>0恒成立,∴u(x)在(1,+∞)上是增函数,∴u(x)>u(1)=-1,
∴
>-1,即
的取值范围为(-1,+∞).
| b |
| x |
∵g(x)≥1在x∈(0,+∞)上恒成立,
∴b≤x2-2x-
| x |
| ex |
记h(x)=x2-2x-
| x |
| ex |
| (x-1)(2ex+1) |
| ex |
当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数;
∴h(x)min=h(1)=-1-e-1,
∴b的最大值为-1-e-1.
②∵g(x)=(ax-
| b |
| x |
∴g′(x)=(
| b |
| x2 |
| b |
| x |
∴由g(x)+g′(x)=0,整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g(x)+g′(x)=0成立,
等价于存在x>1,2ax3-3ax2-2bx+b=0成立,
∵a>0,∴
| b |
| a |
| 2x3-3x2 |
| 2x-1 |
设u(x)=
| 2x3-3x2 |
| 2x-1 |
8x[(x-
| ||||
| (2x-1)2 |
∵x>1,∴u′(x)>0恒成立,∴u(x)在(1,+∞)上是增函数,∴u(x)>u(1)=-1,
∴
| b |
| a |
| b |
| a |
点评:本题考查了利用导数的性质,求函数的极值,构造函数,利用化归,等价转化思想,解决恒成立问题和存在性的问题,这是常考的题型,也是高考的热点.平时要多多留意.

练习册系列答案
相关题目
如图(1)、(2)、(3)、(4)是四个几何体的三视图,这四个几何体依次分别是( )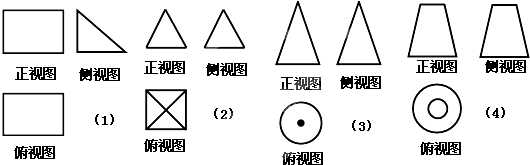

| A、三棱台、三棱柱、圆锥、圆台 |
| B、三棱台、三棱锥、圆锥、圆台 |
| C、三棱柱、四棱锥、圆锥、圆台 |
| D、三棱柱、三棱台、圆锥、圆台 |
 已知函数f(x)=
已知函数f(x)=