题目内容
18.若复数z满足$\frac{1-z}{1+z}=i$,则$|{\overline z+2}|$的值为$\sqrt{5}$.分析 把已知等式变形,再由复数代数形式的乘除运算化简,再由复数求模公式计算得答案.
解答 解:由$\frac{1-z}{1+z}=i$,
得$z=\frac{1-i}{1+i}$=$\frac{(1-i)^{2}}{(1+i)(1-i)}=\frac{-2i}{2}=-i$,
∴$\overline{z}=i$.
则$|{\overline z+2}|$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
8.已知直线$y=\frac{{2\sqrt{3}}}{3}x$和椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$交于不同的两点M,N,若M,N在x轴上的射影恰好为椭圆的两个焦点,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
6.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
3.在极坐标系中,点M(1,0)关于极点的对称点为( )
| A. | (1,0) | B. | (-1,π) | C. | (1,π) | D. | (1,2π) |
10.化简y=$\frac{2sin2α}{1+cos2α}$( )
| A. | tanα | B. | tan2α | C. | 2tanα | D. | 2tan2α |
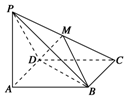 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).