题目内容
若定义：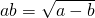
，a?b=|a+b|，则“-2≤x≤2”是“
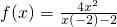有意义”的
- A.充分条件但不是必要条件
- B.必要条件但不是充分条件
- C.充要条件
- D.既不充分也不必要条件
B
分析：由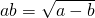，a?b=|a+b|，知=
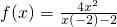，故f（x）的定义域是
，由此得到“-2≤x≤2”是“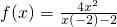有意义”的必要不充分条件．
解答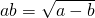：∵，a?b=|a+b|，
∴=，
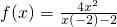∴f（x）的定义域是，
解得-2≤x＜0，或0＜x≤2．
∵x=0时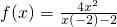，无意义，
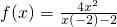“有意义”?x≠0．
所以“-2≤x≤2”是“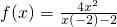有意义”的必要不充分条件．
故选B．
点评：本题考查必要条件、充分条件、充要条件的性质和应用，是基础题．解题时要认真审题，仔细解答．
分析：由
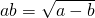，a?b=|a+b|，知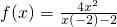=，故f（x）的定义域是，由此得到“-2≤x≤2”是“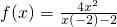有意义”的必要不充分条件．解答：∵
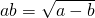，a?b=|a+b|，∴
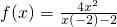=，∴f（x）的定义域是
，解得-2≤x＜0，或0＜x≤2．
∵x=0时，
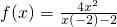无意义，“
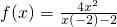有意义”?x≠0．所以“-2≤x≤2”是“
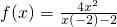有意义”的必要不充分条件．故选B．
点评：本题考查必要条件、充分条件、充要条件的性质和应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
若定义运算f(a*b)=
，则函数f(log2(1+x)*log2(1-x))的值域是（ ）
|
| A、（-1，1） |
| B、[0，1） |
| C、[0，+∞） |
| D、[0，1] |
若定义运算：a?b=
；，例如2?3=3，则下列等式不能成立的是（ ）
|
| A、a?b=b?a |
| B、（a?b）?c=a?（b?c） |
| C、（a?b）2=a2?b2 |
| D、c•（a?b）=（c•a）?（c•b）（c＞0） |
，a?b=|a+b|，则“-2≤x≤2”是“
有意义”的（ ）