题目内容
函数y=tan(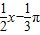 )在一个周期内的图象是( )
)在一个周期内的图象是( )A.
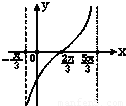
B.
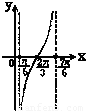
C.
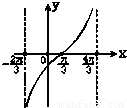
D.
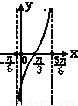
【答案】分析:先令tan(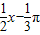 )=0求得函数的图象的中心,排除C,D;再根据函数y=tan(
)=0求得函数的图象的中心,排除C,D;再根据函数y=tan(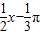 )的最小正周期为2π,排除B.
)的最小正周期为2π,排除B.
解答:解:令tan(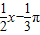 )=0,解得x=kπ+
)=0,解得x=kπ+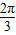 ,可知函数y=tan(
,可知函数y=tan(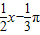 )与x轴的一个交点不是
)与x轴的一个交点不是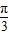 ,排除C,D
,排除C,D
∵y=tan(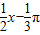 )的周期T=
)的周期T=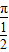 =2π,故排除B
=2π,故排除B
故选A
点评:本题主要考查了正切函数的图象.要熟练掌握正切函数的周期,单调性,对称中心等性质.
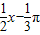 )=0求得函数的图象的中心,排除C,D;再根据函数y=tan(
)=0求得函数的图象的中心,排除C,D;再根据函数y=tan(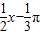 )的最小正周期为2π,排除B.
)的最小正周期为2π,排除B.解答:解:令tan(
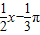 )=0,解得x=kπ+
)=0,解得x=kπ+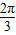 ,可知函数y=tan(
,可知函数y=tan(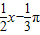 )与x轴的一个交点不是
)与x轴的一个交点不是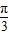 ,排除C,D
,排除C,D∵y=tan(
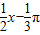 )的周期T=
)的周期T=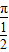 =2π,故排除B
=2π,故排除B故选A
点评:本题主要考查了正切函数的图象.要熟练掌握正切函数的周期,单调性,对称中心等性质.

练习册系列答案
相关题目
若函数y=tan(ωx+
)在[-
,
]上单调递减,且在[-
,
]上的最大值为
,则ω的值为( )
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
