题目内容
10.已知边长为$\sqrt{3}$的正三角形ABC三个顶点都在球O的表面上,且球心O到平面ABC的距离为该球半径的一半,则球O的表面积为$\frac{16π}{3}$.分析 设OO′⊥平面ABC,垂足是O′,设球半径为r,则AO′=1,OA=r,OO′=$\frac{1}{2}r$,由勾股定理求出r2=$\frac{4}{3}$,由此能求出球O的表面积.
解答 解: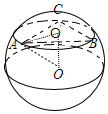 如图,设OO′⊥平面ABC,垂足是O′,设球半径为r,
如图,设OO′⊥平面ABC,垂足是O′,设球半径为r,
∵边长为$\sqrt{3}$的正三角形ABC三个顶点都在球O的表面上,
且球心O到平面ABC的距离为该球半径的一半,
∴AO′=$\frac{2}{3}\sqrt{3-\frac{3}{4}}$=1,OA=r,OO′=$\frac{1}{2}r$,
∵OA2=O′A2+OO'2,∴${r}^{2}=1+\frac{{r}^{2}}{4}$
解得r2=$\frac{4}{3}$,
∴球O的表面积S=4πr2=$\frac{16π}{3}$.
故答案为:$\frac{16π}{3}$.
点评 本题考查球的表面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
20.已知{an}是各项均为正数的等比数列(公比q>1),bn=log2an,b1+b2+b3=3,b1b2b3=-3,则an=( )
| A. | ${a_n}={2^{2n-3}}$ | B. | ${a_n}={2^{5-2n}}$ | ||
| C. | ${a_n}={2^{2n-5}}$ | D. | ${a_n}={2^{2n-3}}$或${a_n}={2^{5-2n}}$ |
1.一超市在销售一批大小相近的某时令水果时,由于存放的时间对口味影响较大,超市根据调研决定最多销售5天,第6天就会扎成果汁.进价2元一个,售价10元一个,每天的仓储保管费平均为每个水果每天0.5元,(第一天售出的水果,算一天仓储保管费,第二天售出的水果,算两天仓储保管费,以此类推)一个水果榨成果汁后能卖2元且能很快售完,果汁不计仓储保管成本.按以下规则定价:
从该批水果中随机抽取100个贴上标记,根据这100个水果的销售情况得到如下数据:
(1)①估计一个水果至多两天(包括两天)销售出去的概率;
②若一个水果在第二天售出,求这个水果产生的利润.
(2)以事件发生的频率作为相应的概率,在这批水果的销售活动中,设一个水果产生的利润为X元,求X的分布列和数学期望E(X)
| 售出时间 | 第一天 | 第二天 | 第三天 | 第四天 | 第五天 |
| 售出时折扣 | 原价 | 9折 | 8折 | 7折 | 5折 |
| 售出的时间 | 第一天 | 第二天 | 第三天 | 第四天 | 第五天 |
| 售出的个数 | 40 | 25 | 15 | 5 | 10 |
②若一个水果在第二天售出,求这个水果产生的利润.
(2)以事件发生的频率作为相应的概率,在这批水果的销售活动中,设一个水果产生的利润为X元,求X的分布列和数学期望E(X)
5.△ABC的内角A,B,C的对边分别为a,b,c.已知a=1,c=2,$cosC=\frac{1}{4}$,则△ABC的面积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\frac{{\sqrt{15}}}{8}$ |
20.设集合A={x|-1<x<3},B={y|y=2x,x∈[0,2]},则A∩B=( )
| A. | [0,2] | B. | (1,3) | C. | [1,3) | D. | (1,4) |