题目内容
若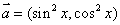 ,
,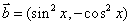 ,
,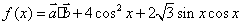 .
.
如果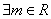 ,对
,对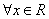 都有
都有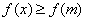 ,则
,则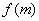 等于
等于
A.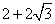 B.
B.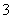 C.
C.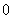 D.
D.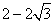
C

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
题目内容
若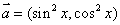 ,
,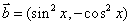 ,
,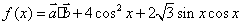 .
.
如果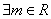 ,对
,对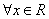 都有
都有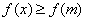 ,则
,则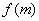 等于
等于
A.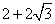 B.
B.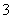 C.
C.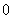 D.
D.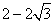
C

 通城学典默写能手系列答案
通城学典默写能手系列答案