题目内容
在△ABC中,已知a2+b2=2013c2,求证:
为定值.
| 2sinAsinBcosC |
| sin2(A+B) |
考点:三角函数恒等式的证明
专题:解三角形
分析:由a2+b2=2013c2,利用余弦定理可得a2+b2-c2=2012c2=2abcosC.利用诱导公式和两角和正弦定理可得
=
=
=2012.
| 2sinAsinBcosC |
| sin2(A+B) |
| 2sinAsinBcosC |
| sin2C |
| 2ab•cosC |
| c2 |
解答:
证明:∵a2+b2=2013c2,
∴a2+b2-c2=2012c2=2abcosC.
∴
=
=
=2012
∴a2+b2-c2=2012c2=2abcosC.
∴
| 2sinAsinBcosC |
| sin2(A+B) |
| 2sinAsinBcosC |
| sin2C |
| 2ab•cosC |
| c2 |
点评:本题考查了三角函数诱导公式、正弦定理等基础知识与基本技能方法,难度中档.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
已知函数f(x)=
,若f(t)+f(t+2)>0,则实数t的取值范围是( )
|
A、t<-3-
| ||||
| B、t>-1 | ||||
C、t<1-
| ||||
| D、t<-2 |
已知△ABC为等边三角形,AB=2,设点P,Q满足
=λ
,
=(1-λ)
,λ∈R,若
•
=-
,则λ=( )
| AP |
| AB |
| AQ |
| AC |
| BQ |
| CP |
| 5 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知线段AB、BD在平面α内,∠ABD=120°,线段AC⊥α,如果AB=a,BD=b,AC=c,则线段CD的长为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
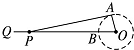 如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于
如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于