题目内容
如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG∶GC=DH∶HC=1∶2.
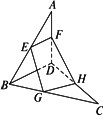
(1)求证:E、F、H、G四点共面.
(2)设EG与HF交于点P,求证:P、A、C三点共线.
答案:
解析:
解析:
|
思路解析:根据比例相等,证明两直线平行,从而确定平面;证明三点共线时,先证明两个平面相交,再证第三个点也在这条交线上即可. 解:(1)∵E、F分别是AB、AD的中点, ∴EF∥BD. 在△BCD中,∵ ∴GH∥BD. ∴EF∥HG. ∴E、F、H、G四点共面. (2)设EG∩HF=P,则P∈平面ABC,P∈平面ACD,∴P为平面ABC与平面ACD的公共点.又平面ABC∩平面ACD=AC, ∴P、A、C三点共线. |

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
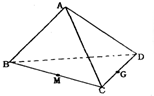 如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则
如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H. 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且
如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且 如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2
如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2