题目内容
设f(x)=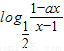 为奇函数,a为常数.
为奇函数,a为常数.(1)求a的值;并判断f(x)在区间(1,+∞)上的单调性;
(2)若对于区间(3,4)上的每一个x的值,不等式f(x)>
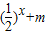 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】分析:(1)由奇函数的定义域关于原点对称可求得a值,根据单调性的定义及复合函数单调性的判定方法可判断f(x)的单调性;
(2)不等式f(x)>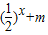 恒成立,等价于f(x)-
恒成立,等价于f(x)-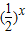 >m恒成立,构造函数g(x)=f(x)-
>m恒成立,构造函数g(x)=f(x)-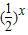 ,x∈(3,4),转化为求函数g(x)在(3,4)上的最值问题即可解决.
,x∈(3,4),转化为求函数g(x)在(3,4)上的最值问题即可解决.
解答:解:(1)∵f(x)是奇函数,∴定义域关于原点对称,
由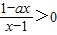 ,得(x-1)(1-ax)>0.
,得(x-1)(1-ax)>0.
令(x-1)(1-ax)=0,得x1=1,x2=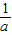 ,∴
,∴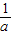 =-1,解得a=-1.
=-1,解得a=-1.
令u(x)=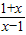 =1+
=1+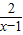 ,设任意x1<x2,且x1,x2∈(1,+∞),
,设任意x1<x2,且x1,x2∈(1,+∞),
则u(x1)-u(x2)=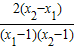 ,
,
∵1<x1<x2,∴x1-1>0,x2-1>0,x2-x1>0,
∴u(x1)-u(x2)>0,即u(x1)>u(x2).
∴u(x)=1+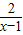 (x>1)是减函数,
(x>1)是减函数,
又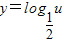 为减函数,
为减函数,
∴f(x)=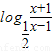 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
(2)由题意知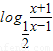 -
-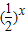 >m,x∈(3,4)时恒成立,
>m,x∈(3,4)时恒成立,
令g(x)=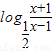 -
-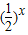 ,x∈(3,4),由(1)知
,x∈(3,4),由(1)知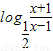 在[3,4]上为增函数,
在[3,4]上为增函数,
又-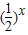 在(3,4)上也是增函数,故g(x)在(3,4)上为增函数,
在(3,4)上也是增函数,故g(x)在(3,4)上为增函数,
∴g(x)的最小值为g(3)=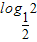 -
-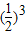 =-
=- ,
,
∴m≤- ,故实数m的范围是(-∞,-
,故实数m的范围是(-∞,- ].
].
点评:本题考查函数的单调性、奇偶性及函数恒成立问题,奇偶性、单调性问题常用定义解决,而函数恒成立问题则常转化为最值问题处理.
(2)不等式f(x)>
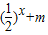 恒成立,等价于f(x)-
恒成立,等价于f(x)-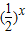 >m恒成立,构造函数g(x)=f(x)-
>m恒成立,构造函数g(x)=f(x)-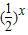 ,x∈(3,4),转化为求函数g(x)在(3,4)上的最值问题即可解决.
,x∈(3,4),转化为求函数g(x)在(3,4)上的最值问题即可解决.解答:解:(1)∵f(x)是奇函数,∴定义域关于原点对称,
由
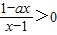 ,得(x-1)(1-ax)>0.
,得(x-1)(1-ax)>0.令(x-1)(1-ax)=0,得x1=1,x2=
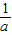 ,∴
,∴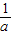 =-1,解得a=-1.
=-1,解得a=-1.令u(x)=
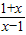 =1+
=1+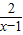 ,设任意x1<x2,且x1,x2∈(1,+∞),
,设任意x1<x2,且x1,x2∈(1,+∞),则u(x1)-u(x2)=
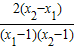 ,
,∵1<x1<x2,∴x1-1>0,x2-1>0,x2-x1>0,
∴u(x1)-u(x2)>0,即u(x1)>u(x2).
∴u(x)=1+
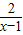 (x>1)是减函数,
(x>1)是减函数,又
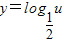 为减函数,
为减函数,∴f(x)=
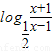 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.(2)由题意知
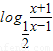 -
-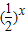 >m,x∈(3,4)时恒成立,
>m,x∈(3,4)时恒成立,令g(x)=
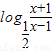 -
-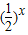 ,x∈(3,4),由(1)知
,x∈(3,4),由(1)知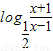 在[3,4]上为增函数,
在[3,4]上为增函数,又-
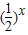 在(3,4)上也是增函数,故g(x)在(3,4)上为增函数,
在(3,4)上也是增函数,故g(x)在(3,4)上为增函数,∴g(x)的最小值为g(3)=
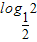 -
-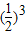 =-
=- ,
,∴m≤-
 ,故实数m的范围是(-∞,-
,故实数m的范围是(-∞,- ].
].点评:本题考查函数的单调性、奇偶性及函数恒成立问题,奇偶性、单调性问题常用定义解决,而函数恒成立问题则常转化为最值问题处理.

练习册系列答案
相关题目
设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则xf(x)<0的解集为( )
| A、(-1,0)∪(2,+∞) | B、(-∞,-2)∪(0,2) | C、(-∞,-2)∪(2,+∞) | D、(-2,0)∪(0,2 |