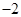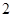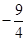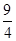题目内容
已知函数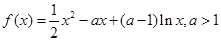 ,
,
(1)讨论函数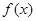 的单调性;
的单调性;
(2)证明:若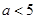 ,则对于任意
,则对于任意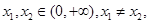 有
有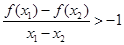 。
。
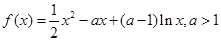 ,
,(1)讨论函数
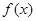 的单调性;
的单调性;(2)证明:若
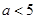 ,则对于任意
,则对于任意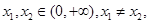 有
有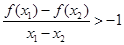 。
。(1)a=2时,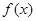 在
在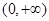 上单调增加;
上单调增加;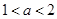 时,
时,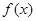 在
在 上单调减少,在
上单调减少,在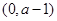 ,
,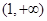 上单调增加;
上单调增加;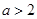 时,
时,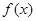 在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加;
在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加;
(2)证明详见解析
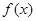 在
在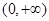 上单调增加;
上单调增加;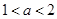 时,
时,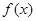 在
在 上单调减少,在
上单调减少,在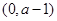 ,
,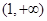 上单调增加;
上单调增加;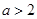 时,
时,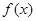 在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加;
在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加; (2)证明详见解析
试题分析:(1)求导,利用导数分类求单调性;(2)先求导,然后求出单间区间,在进一步证明即可.
试题解析:(1)
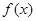 的定义域为
的定义域为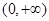 ,
,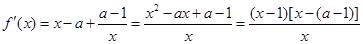
(i)若
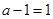 ,即a=2,则
,即a=2,则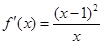 ,故
,故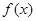 在
在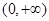 上单调增加。
上单调增加。(ii)若
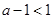 ,而
,而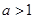 ,故
,故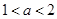 ,则当
,则当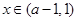 时,
时,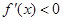 ;
;当
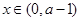 及
及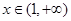 时,
时,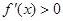 。
。故
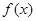 在
在 上单调减少,在
上单调减少,在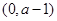 ,
,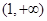 上单调增加。
上单调增加。(iii)若
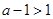 ,即
,即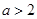 , 同理可得
, 同理可得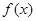 在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加。
在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加。 (2)考虑函数
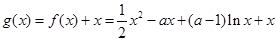 ,
,则
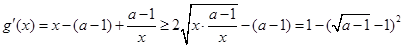 ,
,由于
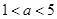 ,故
,故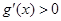 ,即
,即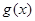 在
在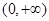 上单调增加,从而当
上单调增加,从而当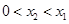 时,
时,有
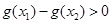 ,即
,即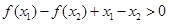 ,故
,故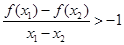 ;
;当
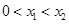 时,有
时,有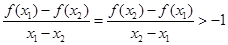 。
。
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

 的值域;
的值域; ,函数
,函数 .若对任意
.若对任意 ,总存在
,总存在 ,使
,使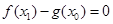 ,求实数
,求实数 的取值范围.
的取值范围.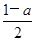
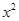 +ax-lnx(a∈R).
+ax-lnx(a∈R).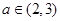 及任意
及任意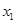 ,
,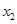 ∈[1,2],恒有
∈[1,2],恒有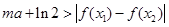 成立,求实数m的取值范围.
成立,求实数m的取值范围. ,
,
 的周期和对称中心;
的周期和对称中心; 上值域.
上值域.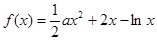
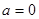 时,求
时,求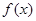 的极值;
的极值; 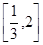 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.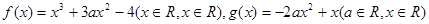 (Ⅰ)若函数
(Ⅰ)若函数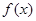 在
在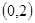 上单调递减,在区间
上单调递减,在区间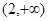 单调递增,求
单调递增,求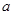 的值;
的值;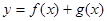 在
在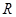 上有两个不同的极值点,求
上有两个不同的极值点,求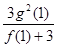 的取值范围;
的取值范围;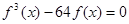 有且只有三个不同的实根,求
有且只有三个不同的实根,求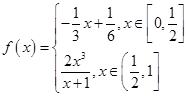 ,函数
,函数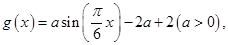 若存在
若存在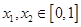 ,使得
,使得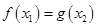 成立,则实数
成立,则实数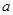 的取值范围( )
的取值范围( )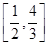
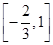
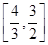

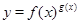 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: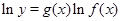 ,再两边同时求导得
,再两边同时求导得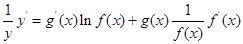 ,于是得到:
,于是得到: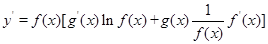 ,运用此方法求得函数
,运用此方法求得函数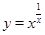 的一个单调递增区间是( )
的一个单调递增区间是( )


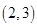
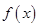 的导数为
的导数为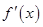 ,且满足关系式
,且满足关系式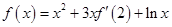 则
则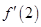 的值等于( )
的值等于( )