题目内容
(本小题12分)设函数 ,
,
(1)求 的周期和对称中心;
的周期和对称中心;
(2)求 在
在 上值域.
上值域.
 ,
,
(1)求
 的周期和对称中心;
的周期和对称中心;(2)求
 在
在 上值域.
上值域.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)先求
 ,再求g(x)的解析式,然后根据正弦型函数的性质,求周期和对称中心;
,再求g(x)的解析式,然后根据正弦型函数的性质,求周期和对称中心;(2)由x

 ,求出
,求出 ,再由正弦函数的性质即可求出所求值域.
,再由正弦函数的性质即可求出所求值域.试题解析:(1)
 =cosx-sinx,
=cosx-sinx,
=(cosx+sinx)(cosx-sinx)+(cosx+sinx)2=

所以g(x)的周期T=
 ,
,由
 得
得 
所以
 的对称中心为
的对称中心为
(2)因为
 ,所以
,所以 ,
,
所以



练习册系列答案
相关题目
 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数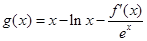 的最小值为1,其中
的最小值为1,其中 是函数f(x)的导数.
是函数f(x)的导数.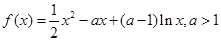 ,
,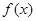 的单调性;
的单调性;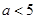 ,则对于任意
,则对于任意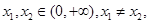 有
有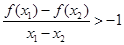 。
。
 ,求
,求 的单调区间,
的单调区间, 时,
时, ,求
,求 的取值范围.
的取值范围.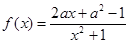 ,其中
,其中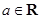 .
.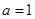 时,记
时,记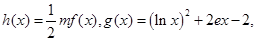 存在
存在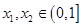 使
使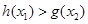 成立,求实数
成立,求实数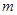 的取值范围;
的取值范围;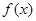 在
在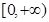 上存在最大值和最小值,求
上存在最大值和最小值,求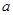 的取值范围.
的取值范围.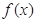 =
=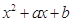 ,
,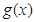 =
=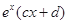 ,若曲线
,若曲线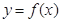 和曲线
和曲线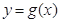 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线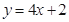 .
.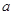 ,
,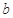 ,
,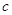 ,
,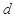 的值;
的值;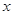 ≥-2时,
≥-2时,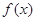 ≤
≤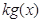 ,求
,求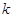 的取值范围.
的取值范围.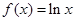 ,
,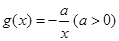
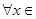 (0,e],都有f(x)≥g(x)+
(0,e],都有f(x)≥g(x)+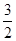 ,求实数a的取值范围.
,求实数a的取值范围.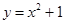 在点
在点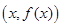 处的切线的斜率为
处的切线的斜率为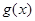 ,则函数
,则函数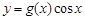 的部分图象可以为( )
的部分图象可以为( )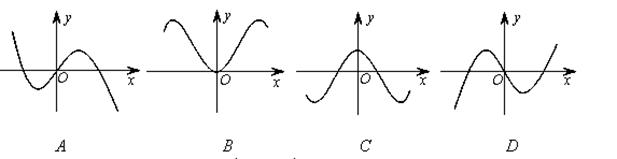
 ,其中
,其中 ,则
,则 是偶函数的充要条件是( )
是偶函数的充要条件是( )


