题目内容
已知函数
(1)求 的值域;
的值域;
(2)设 ,函数
,函数 .若对任意
.若对任意 ,总存在
,总存在 ,使
,使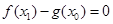 ,求实数
,求实数 的取值范围.
的取值范围.

(1)求
 的值域;
的值域;(2)设
 ,函数
,函数 .若对任意
.若对任意 ,总存在
,总存在 ,使
,使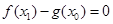 ,求实数
,求实数 的取值范围.
的取值范围.(1)  ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)求出
 的导函数,令导函数等于求出
的导函数,令导函数等于求出 的值,然后由
的值,然后由 的值,分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值即可得到
的值,分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值即可得到 的值域;(2)设函数
的值域;(2)设函数 在[0,2]上的值域是A,根据题意对任意
在[0,2]上的值域是A,根据题意对任意 ,总存在
,总存在 ,使
,使 ,得到区间
,得到区间 是A的子集,求出
是A的子集,求出 的导函数,分
的导函数,分 小于0和
小于0和 大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于
大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于 的不等式,求出不等式的解集即可得到满足题意
的不等式,求出不等式的解集即可得到满足题意 的取值范围.
的取值范围.试题解析:(1)
 ,令
,令 ,得
,得 或
或 .
. 当
 时,
时, 在
在 上单调递增;
上单调递增;当
 时,
时, 在
在 上单调递减,
上单调递减,而
 ,
, 当
当 时,
时, 的值域是
的值域是 .
. (2)设函数
 在
在 上的值域是A,
上的值域是A, 若对任意
若对任意 .总存在
.总存在 1,使
1,使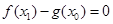 ,
, .
.  .
.①当
 时,
时, ,
, 函数
函数 在
在 上单调递减.
上单调递减.  ,当
,当 时,不满足
时,不满足 ;
;②当
 时,
时, ,令
,令 ,得
,得 或
或 (舍去)
(舍去) (i)
 时,
时, 的变化如下表:
的变化如下表: | 0 |  |  |  | 2 |
 | | - | 0 | + | |
 | 0 |  |  |  |  |
 .
.
 ,解得
,解得 .
. (ii)当
 时,
时, ,
, 函数
函数 在
在 上单调递减.
上单调递减.
 ,
, 当
当 时,不满
时,不满 .
.综上可知,实数
 的取值范围是
的取值范围是 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
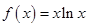 .
.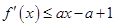 恒成立,求实数a的集合.
恒成立,求实数a的集合. (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数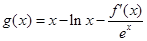 的最小值为1,其中
的最小值为1,其中 是函数f(x)的导数.
是函数f(x)的导数.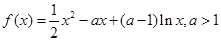 ,
,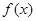 的单调性;
的单调性;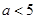 ,则对于任意
,则对于任意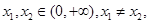 有
有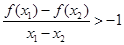 。
。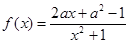 ,其中
,其中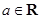 .
.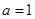 时,记
时,记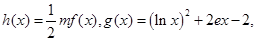 存在
存在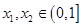 使
使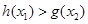 成立,求实数
成立,求实数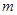 的取值范围;
的取值范围;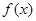 在
在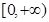 上存在最大值和最小值,求
上存在最大值和最小值,求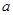 的取值范围.
的取值范围.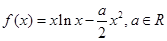
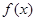 在(0,
在(0,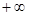 )单调递减,求a的最小值
)单调递减,求a的最小值 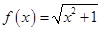 ,对任意
,对任意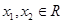 ,恒有
,恒有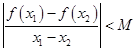 ,其中M是常数,则M的最小值是 .
,其中M是常数,则M的最小值是 . ,其中
,其中 ,则
,则 是偶函数的充要条件是( )
是偶函数的充要条件是( )



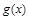 为三次函数
为三次函数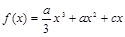 的导函数,则函数
的导函数,则函数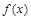 的图像可能是( )
的图像可能是( )