题目内容
16.已知实数x满足32x-4-$\frac{10}{3}$•3x-1+9≤0,且$f(x)={log_2}\frac{x}{2}•{log_2}\frac{{\sqrt{x}}}{2}$.(1)求实数x的取值范围;
(2)求f(x)的最大值和最小值,并求此时x的值.
分析 (1)转化为二次不等式求解即可.
(2)根据对数的运算法则,化简f(x),利用换元法,转化为二次函数求解值域.
解答 解:(1)由32x-4-$\frac{10}{3}$•3x-1+9≤0,
得32x-4-10•3x-2+9≤0,
即(3x-2-1)(3x-2-9)≤0,
∴1≤3x-2≤9,
∴2≤x≤4,
∴实数x的取值范围[2,4]
(2)∵$f(x)={log_2}\frac{x}{2}•{log_2}\frac{{\sqrt{x}}}{2}$=(log2x-1)($\frac{1}{2}$log2x-1)=$\frac{1}{2}$(log2x-1)(log2x-2),
设log2x=t,则t∈[1,2],
∴f(t)=$\frac{1}{2}$(t-1)(t-2)=$\frac{1}{2}$(t2-3t+2)=$\frac{1}{2}$(t-$\frac{3}{2}$)2-$\frac{1}{8}$,
∵f(t)在[1,$\frac{3}{2}$]上递减,在[$\frac{3}{2}$,2]上递增,
∴f(x)min=f(t)min=f($\frac{3}{2}$)=-$\frac{1}{8}$,此时log2x=$\frac{3}{2}$,解得x=2$\sqrt{2}$,
f(x)max=f(t)max=f(1)=f(2)=0,此时当log2x=1或log2x=2,即x=2或x=4时.
点评 本题考查了指数的运算和对数的运算,转化思想,利用二次函数的配方求解最值问题,是一道中档题.

练习册系列答案
相关题目
4. 中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )
 中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅造的一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取为3,其体积为12.6(立方升),则三视图中x的为( )| A. | 3.4 | B. | 4.0 | C. | 3.8 | D. | 3.6 |
1.已知四面体P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=$\sqrt{3}$AB,若四面体P-ABC 的体积为$\frac{3}{2}$,求球的表面积( )
| A. | 8π | B. | 12π | C. | 8$\sqrt{3}$π | D. | 12$\sqrt{3}$π |
8.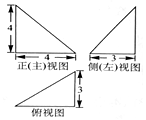 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )
 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )| A. | 8 | B. | 10 | C. | 20 | D. | 24 |
5.在△abc中,三边之比a:b:c=2:3:4,则$\frac{sinA-2sinB}{sinC}$=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |