题目内容
4.在△ABC中,角A、B、C的对边分别为a、b、c,$\frac{π}{3}$-A=B,a=3,b=5,则c=7.分析 由已知及三角形内角和定理可求C的值,进而利用余弦定理即可求得c的值.
解答 解:∵$\frac{π}{3}$-A=B,A+B+C=π,
∴C=$\frac{2π}{3}$,
又∵a=3,b=5,
∴由余弦定理可得:c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{{3}^{2}+{5}^{2}-2×3×5×(-\frac{1}{2})}$=7.
故答案为:7.
点评 本题主要考查了三角形内角和定理,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
12.一平面过半径为R的球O的半径OA的中点,且垂直于该半径OA,则该平面截球的截面面积为( )
| A. | $\frac{1}{2}π{R^2}$ | B. | $\frac{{\sqrt{3}}}{2}π{R^2}$ | C. | πR2 | D. | $\frac{3}{4}π{R^2}$ |
9.等差数列{an}和{bn},其前n项和分别为Sn,Tn,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+2}{n+3}$,则$\frac{{{a_{10}}}}{{{b_{10}}}}$等于( )
| A. | $\frac{72}{13}$ | B. | $\frac{135}{22}$ | C. | $\frac{79}{14}$ | D. | $\frac{142}{23}$ |
14.已知a>b,则下列不等式正确的是( )
| A. | ac>bc | B. | a2>b2 | C. | |a|<|b| | D. | 2a>2b |
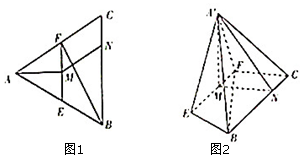 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.