题目内容
函数
（x∈R）。
（1）求函数f(x)的值域；
（2）判断并证明函数f(x)的单调性；
（3）判断并证明函数f(x)的奇偶性；
（4）解不等式f(1-m)+f(1-m2)＜0。
（x∈R）。（1）求函数f(x)的值域；
（2）判断并证明函数f(x)的单调性；
（3）判断并证明函数f(x)的奇偶性；
（4）解不等式f(1-m)+f(1-m2)＜0。
解：（1）
，
又
，
∴-1＜y＜1，
即函数f(x)的值域为(-1，1)。
（2）函数f(x)在R上为单调增函数。
证明：
，
在定义域中任取两个实数x1，x2，且x1＜x2，
则
，
，
∴
，从而
，
∴函数f(x)在R上为单调增函数。
（3）
，
∴函数f(x)为奇函数。
（4）由（3）知，函数f(x)为奇函数，
∴
，即
，
∴
，
即
，解得：m＜-2或m＞1，
∴原不等式的解集为
。
，又
，∴-1＜y＜1，
即函数f(x)的值域为(-1，1)。
（2）函数f(x)在R上为单调增函数。
证明：
，在定义域中任取两个实数x1，x2，且x1＜x2，
则
，，∴
，从而， ∴函数f(x)在R上为单调增函数。
（3）
，∴函数f(x)为奇函数。
（4）由（3）知，函数f(x)为奇函数，
∴
，即，∴
，即
，解得：m＜-2或m＞1，∴原不等式的解集为
。
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
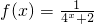（x∈R）．
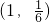在f（x）的图象上，判断其关于点
对称的点是否仍在f（x）的图象上；
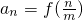（m∈{N}^{*}，n=1，2，…，m），求数列{an}的前m项和Sm．
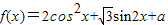（x∈R）．
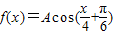，x∈R，且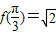
，
，
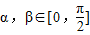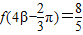，求cos（α+β）的值．
（x∈R）．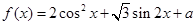
（x∈R）．
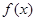有最大值2，求实数a的值；