题目内容
已知函数 (x∈R).
(x∈R).(1)若f(x)有最大值2,求实数a的值;
(2)求函数f(x)的单调递增区间.
【答案】分析:(1)先利用二倍角公式和两角和公式对函数解析式化简整理,根据正弦函数的性质求得函数的最大值的表达式,进而根据最大值为2求得a的值.
(2)令 求得x的范围,进而确定函数的单调递增区间.
求得x的范围,进而确定函数的单调递增区间.
解答:解:(1) ,
,
当 (k∈Z)时,f(x)有最大值,
(k∈Z)时,f(x)有最大值,
即 (k∈Z)时,f(x)有最大值为3+a,
(k∈Z)时,f(x)有最大值为3+a,
∴3+a=2,解得a=-1.
(2)令 ,解得
,解得 (k∈Z),
(k∈Z),
∴函数f(x)的单调递增区间 (k∈Z)
(k∈Z)
点评:本题主要考查了二倍角公式的应用,以及正弦函数的基本性质.解题的关键是利用二倍角公式和两角和公式对函数解析式化简整理.
(2)令
 求得x的范围,进而确定函数的单调递增区间.
求得x的范围,进而确定函数的单调递增区间.解答:解:(1)
 ,
,当
 (k∈Z)时,f(x)有最大值,
(k∈Z)时,f(x)有最大值,即
 (k∈Z)时,f(x)有最大值为3+a,
(k∈Z)时,f(x)有最大值为3+a,∴3+a=2,解得a=-1.
(2)令
 ,解得
,解得 (k∈Z),
(k∈Z),∴函数f(x)的单调递增区间
 (k∈Z)
(k∈Z)点评:本题主要考查了二倍角公式的应用,以及正弦函数的基本性质.解题的关键是利用二倍角公式和两角和公式对函数解析式化简整理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.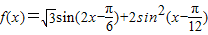 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.