题目内容
已知函数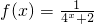 (x∈R).
(x∈R).
(1)已知点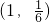 在f(x)的图象上,判断其关于点
在f(x)的图象上,判断其关于点 对称的点是否仍在f(x)的图象上;
对称的点是否仍在f(x)的图象上;
(2)求证:函数f(x)的图象关于点 对称;
对称;
(3)若数列{an}的通项公式为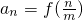 (m∈{N}^{*},n=1,2,…,m),求数列{an}的前m项和Sm.
(m∈{N}^{*},n=1,2,…,m),求数列{an}的前m项和Sm.
解:(1)显然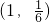 关于点
关于点
的对称点为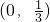 ,满足函数解析式,
,满足函数解析式,
所以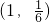 关于点
关于点 的对称点仍在该函数的图象上.(3分)
的对称点仍在该函数的图象上.(3分)
(2)设点P0(x0,y0)是函数f(x)的图象上任意一点,
其关于点 的对称点为P(x,y).
的对称点为P(x,y).
由 得
得
所以,点P的坐标为P .(6分)
.(6分)
由点P0(x0,y0)在函数f(x)的图象上,
得 .
.
∵ ,
,
 =
= ,
,
∴点P 在函数f(x)的图象上.
在函数f(x)的图象上.
∴函数f(x)的图象关于点 对称.(9分)
对称.(9分)
(3)由(2)可知,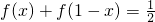 ,
,
所以 ,
,
即 ,∴
,∴ ,(12分)
,(12分)
由Sm=a1+a2+a3++am-1+am,①
得Sm=am-1+am-2+am-3++a1+am,②
由①+②,得 ,
,
∴ .(16分)
.(16分)
分析:(1)由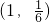 关于点
关于点 的对称点为
的对称点为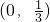 ,满足函数解析式,所以
,满足函数解析式,所以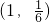 关于点
关于点 的对称点仍在该函数的图象上.
的对称点仍在该函数的图象上.
(2)设点P0(x0,y0)是函数f(x)的图象上任意一点,其关于点 的对称点为P(x,y).由
的对称点为P(x,y).由 得点P的坐标为P
得点P的坐标为P .由点P0(x0,y0)在函数f(x)的图象上,得
.由点P0(x0,y0)在函数f(x)的图象上,得 .由此能够推导出函数f(x)的图象关于点
.由此能够推导出函数f(x)的图象关于点 对称.
对称.
(3)由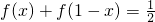 ,知
,知 ,由Sm=a1+a2+a3++am-1+am,得Sm=am-1+am-2+am-3++a1+am,由此能求出数列{an}的前m项和Sm.
,由Sm=a1+a2+a3++am-1+am,得Sm=am-1+am-2+am-3++a1+am,由此能求出数列{an}的前m项和Sm.
点评:本题考查数列的综合应用,解题时要注意公式的合理运用.
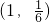 关于点
关于点
的对称点为
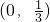 ,满足函数解析式,
,满足函数解析式,所以
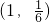 关于点
关于点 的对称点仍在该函数的图象上.(3分)
的对称点仍在该函数的图象上.(3分)(2)设点P0(x0,y0)是函数f(x)的图象上任意一点,
其关于点
 的对称点为P(x,y).
的对称点为P(x,y).由
 得
得
所以,点P的坐标为P
 .(6分)
.(6分)由点P0(x0,y0)在函数f(x)的图象上,
得
 .
.∵
 ,
, =
= ,
,∴点P
 在函数f(x)的图象上.
在函数f(x)的图象上.∴函数f(x)的图象关于点
 对称.(9分)
对称.(9分)(3)由(2)可知,
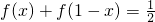 ,
,所以
 ,
,即
 ,∴
,∴ ,(12分)
,(12分)由Sm=a1+a2+a3++am-1+am,①
得Sm=am-1+am-2+am-3++a1+am,②
由①+②,得
 ,
,∴
 .(16分)
.(16分)分析:(1)由
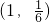 关于点
关于点 的对称点为
的对称点为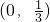 ,满足函数解析式,所以
,满足函数解析式,所以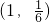 关于点
关于点 的对称点仍在该函数的图象上.
的对称点仍在该函数的图象上.(2)设点P0(x0,y0)是函数f(x)的图象上任意一点,其关于点
 的对称点为P(x,y).由
的对称点为P(x,y).由 得点P的坐标为P
得点P的坐标为P .由点P0(x0,y0)在函数f(x)的图象上,得
.由点P0(x0,y0)在函数f(x)的图象上,得 .由此能够推导出函数f(x)的图象关于点
.由此能够推导出函数f(x)的图象关于点 对称.
对称.(3)由
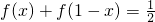 ,知
,知 ,由Sm=a1+a2+a3++am-1+am,得Sm=am-1+am-2+am-3++a1+am,由此能求出数列{an}的前m项和Sm.
,由Sm=a1+a2+a3++am-1+am,得Sm=am-1+am-2+am-3++a1+am,由此能求出数列{an}的前m项和Sm.点评:本题考查数列的综合应用,解题时要注意公式的合理运用.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.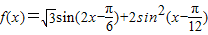 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.