题目内容
在数列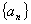 中,
中,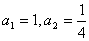 ,且
,且 .
.
(Ⅰ) 求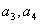 ,猜想
,猜想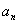 的表达式,并加以证明;
的表达式,并加以证明;
(Ⅱ)设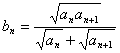 ,求证:对任意的自然数
,求证:对任意的自然数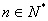 都有
都有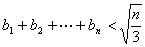 .
.
(Ⅰ) 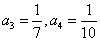 ,
,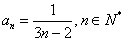 (Ⅱ)
(Ⅱ)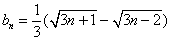
所以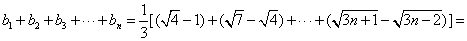
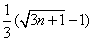 所以只需要证明
所以只需要证明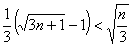
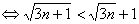
 (显然成立),所以命题得证
(显然成立),所以命题得证
解析试题分析:(Ⅰ)容易求得: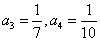 . 1分
. 1分
故可以猜想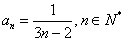 .下面利用数学归纳法加以证明:
.下面利用数学归纳法加以证明:
显然当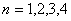 时,结论成立. 2分
时,结论成立. 2分
假设当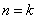 ;
; 时(也可以
时(也可以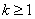 ),结论也成立,即
),结论也成立,即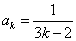 ,
,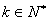 . 3分
. 3分
那么当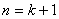 时,由题设与归纳假设可知:
时,由题设与归纳假设可知: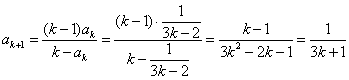
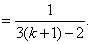 4分
4分
即当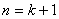 时,结论也成立,综上,对
时,结论也成立,综上,对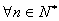 ,
,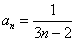 成立. 6分
成立. 6分
(Ⅱ)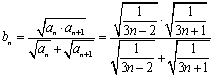
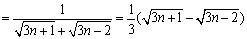 , 8分
, 8分
所以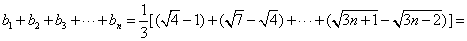
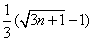 . 10分
. 10分
所以只需要证明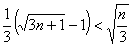
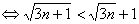
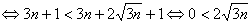 (显然成立)
(显然成立)
所以对任意的自然数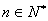 ,都有
,都有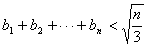 . 12分
. 12分
考点:数学归纳法及数列求和
点评:数学归纳法用来证明与正整数有关的题目,证明步骤:1,证明当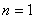 时命题成立。2,假设当
时命题成立。2,假设当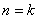 时命题成立,借此证明当
时命题成立,借此证明当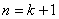 是命题成立,综上1,2得证;数列求和常用的方法有分组求和裂项相消求和错位相减求和等
是命题成立,综上1,2得证;数列求和常用的方法有分组求和裂项相消求和错位相减求和等

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设变量x,y满足约束条件 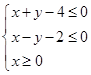 ,则目标函数z=
,则目标函数z=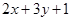 的最大值为
的最大值为
| A.11 | B.10 | C.9. | D.13 |
设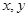 满足约束条件
满足约束条件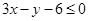 ,
,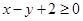 ,
,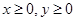 ,若目标函数
,若目标函数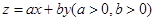 的最大值为12,则
的最大值为12,则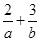 的最小值为( )
的最小值为( )
| A.5 | B.6 | C.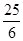 | D.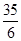 |
 满足
满足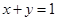 ,求
,求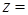
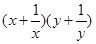 的最小值.
的最小值.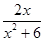 .
.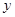 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度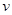 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为
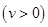
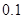 千辆/时)
千辆/时)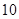 千辆/时,则汽车的平均速度应限定在什么范围内?
千辆/时,则汽车的平均速度应限定在什么范围内?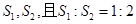 ,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.
,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.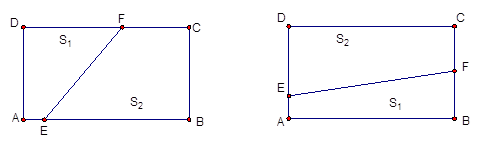
 ,
, ; (2)求
; (2)求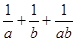 的最小值.
的最小值.