题目内容
交通管理部门为了优化某路段的交通状况,经过对该路段的长期观测发现:在交通繁忙的时段内,该路段内汽车的车流量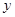 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度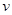 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为
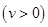
①求在该路段内,当汽车的平均速度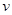 为多少时,车流量最大?最大车流量为多少?(精确到
为多少时,车流量最大?最大车流量为多少?(精确到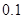 千辆/时)
千辆/时)
②若要求在该时段内车流量超过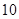 千辆/时,则汽车的平均速度应限定在什么范围内?
千辆/时,则汽车的平均速度应限定在什么范围内?
① 时,
时, (千辆/时)②
(千辆/时)②
解析试题分析:解:①依题意,得 =
=


当且仅当 ,即
,即 时,上式等号成立,
时,上式等号成立,
所以 (千辆/时)
(千辆/时)
②由条件得 ,整理,得
,整理,得
即 ,解得
,解得
答:当 千米/时时,车流量最大,最大车流量约为
千米/时时,车流量最大,最大车流量约为 千辆/时,如果要求在在该时段内车流量超过
千辆/时,如果要求在在该时段内车流量超过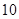 千辆/时,则汽车的平均速度应大于
千辆/时,则汽车的平均速度应大于 千米/时且小于
千米/时且小于 千米/时。
千米/时。
考点:基本不等式;解一元二次不等式
点评:求式子的最值,方法可以结合二次函数、函数的导数、基本不等式和三角函数等。本题就是结合基本不等式。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 ,
, 满足约束条件
满足约束条件 ,若
,若 的最小值为
的最小值为 ,则
,则 ( )
( )
A. | B. | C. | D. |
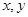 都是正数,
都是正数, ,求
,求 的最大值
的最大值 ,求
,求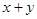 的最小值.
的最小值. ,
, 及
及 的符号;
的符号; ”.
”.  中,
中,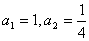 ,且
,且 .
.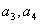 ,猜想
,猜想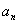 的表达式,并加以证明;
的表达式,并加以证明;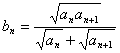 ,求证:对任意的自然数
,求证:对任意的自然数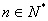 都有
都有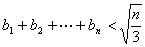 .
. 的最大值为
的最大值为 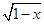 +
+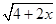 的最大值.
的最大值.