题目内容
7.若将函数y=2sin(4x+ϕ)的图象向右平移$\frac{π}{6}$个单位,得到的图象关于y轴对称,则|ϕ|的最小值是$\frac{π}{6}$.分析 先根据左加右减的原则将函数y=2sin(4x+ϕ)的图象向右平移$\frac{π}{6}$个单位,然后根据图象关于y轴对称,知函数为偶函数,结合诱导公式求出|ϕ|的最小值.
解答 解:将函数y=2sin(4x+ϕ)的图象向右平移$\frac{π}{6}$个单位后得到的图象对应函数为y=2sin(4(x-$\frac{π}{6}$)+φ)=2sin(4x+φ-$\frac{2π}{3}$),
又图象关于y轴对称,所以所得函数为偶函数,
故φ-$\frac{2π}{3}$=kπ+$\frac{π}{2}$(k∈Z),即φ=kπ+$\frac{7π}{6}$(k∈Z),
所以|φ|的最小值为$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题主要考查三角函数图象的平移及三角函数的性质,三角函数的平移原则为左加右减上加下减.三角函数奇偶性的转化结合诱导公式实现.

练习册系列答案
相关题目
2.已知函数$f(x)=\left\{{\begin{array}{l}{cosx-1,x≤0}\\{{{sin}^2}x,x>0}\end{array}}\right.$,则下列结论正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是单调函数 | C. | f(x)是周期函数 | D. | f(x)的值域为[-2,1] |
12.在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
(1)画出频率分布直方图;
(2)估计纤度落在[1.38,1.50)中的频率及纤度小于1.40的频率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
| 分组 | 频数 |
| [1.30,1.34) | 4 |
| [1.34,1.38) | 22 |
| [1.38,1.42) | 40 |
| [1.42,1.46) | 22 |
| [1.46,1.50) | 10 |
| [1.50,1.54) | 2 |
| 合计 | 100 |
(2)估计纤度落在[1.38,1.50)中的频率及纤度小于1.40的频率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
16.如图,点(x,y)在阴影部分所表示的平面区域上,则z=y-x的最大值为( )
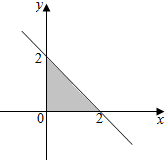

| A. | -2 | B. | 0 | C. | 1 | D. | 2 |