题目内容
已知函数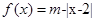 ,
,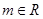 ,且
,且 的解集为
的解集为 .
.
(1)求 的值;
的值;
(2)若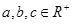 ,且
,且 ,求
,求  的最小值.
的最小值.
(1) ;(2)9.
;(2)9.
解析试题分析:(1)先写出 的解析式,通过解不等式找到
的解析式,通过解不等式找到 的取值范围,又因为解集为
的取值范围,又因为解集为 ,所以让这两个范围相同,所以得出
,所以让这两个范围相同,所以得出 的值;(2)利用柯西不等式求最小值.
的值;(2)利用柯西不等式求最小值.
试题解析:(1)因为 ,
,  等价于
等价于 ,
,
由 有解,得
有解,得 ,且其解集为
,且其解集为 .
.
又 的解集为
的解集为 ,故
,故 . 6分
. 6分
(2)由(1)知 ,又
,又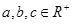 ,由柯西不等式得
,由柯西不等式得 .
.
∴ 的最小值为9 . 12分
的最小值为9 . 12分
考点:1.绝对值不等式的解法;2.柯西不等式.

练习册系列答案
相关题目
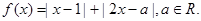 (1)当
(1)当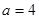 时,求不等式
时,求不等式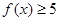 的解集;(2)若
的解集;(2)若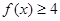 对
对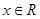 恒成立,求
恒成立,求 的取值范围.
的取值范围. ≥a+b;
≥a+b; (0<x<1)的最小值.?
(0<x<1)的最小值.?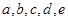 满足
满足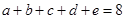 ,
,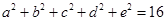 ,试确定
,试确定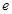 的最大值.
的最大值.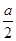 ,
, )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围. 证明:
证明: .
. ,且
,且 ,求证:
,求证:
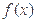 的图象恰好通过
的图象恰好通过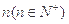 个整点,则称函数
个整点,则称函数 阶整点函数.有下列函数:
阶整点函数.有下列函数: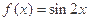 ; ②
; ②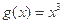 ③
③ ④
④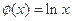 ,
,