题目内容
设函数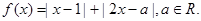 (1)当
(1)当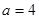 时,求不等式
时,求不等式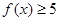 的解集;(2)若
的解集;(2)若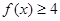 对
对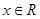 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)  ,(2)
,(2) 
解析试题分析:(1)解含绝对值不等式问题,关键是去绝对值.一般利用绝对值定义分段讨论,因为 ,所以
,所以 或
或 或
或 解得
解得 (2)
(2) 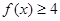 对
对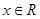 恒成立等价于
恒成立等价于 ,而
,而 ,所以
,所以 ,解得
,解得 或
或 .
.
试题解析:(1)
 ,
, 的解集是
的解集是 . . . (5分)
. . . (5分)
(2) 时,
时,
 时,
时, ,结合
,结合 的图像知,
的图像知, ,解得
,解得 或
或 ,
,
故 的取值范围是
的取值范围是 . (10分)
. (10分)
考点:解含绝对值不等式,不等式恒成立

练习册系列答案
相关题目
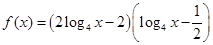 。
。 时,求该函数的值域;
时,求该函数的值域;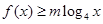 对于
对于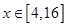 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
- ≥a+
≥a+ -2.
-2. ≤a2+b2+c2<1.
≤a2+b2+c2<1. +
+ +
+ 的最小值.
的最小值. +
+ +
+ ≥6.
≥6.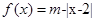 ,
,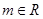 ,且
,且 的解集为
的解集为 .
. 的值;
的值;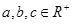 ,且
,且 ,求
,求  的最小值.
的最小值. +
+ +
+ 的最大值.
的最大值.