题目内容
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)等于( )
| A.2 | B.1 | C.-2 | D.-1 |
D
解析试题分析:∵f(x)是R上周期为5的奇函数,∴f(3)=f(3-5)=f(-2)="-f(2)=-2," f(4)=f(4-5)=f(-1)=-f(1)=-1,∴f(3)-f(4)=(-2)-(-1)=-1,故选D
考点:本题考查了函数的性质
点评:熟练掌握函数的奇偶性和周期性是解决此类问题的关键,属基础题

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
下列各组函数中,表示同一函数的是( )
A. | B. |
C. | D. |
已知函数 ,则
,则 ,
,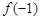 ,
, 的大小关系为
的大小关系为
A.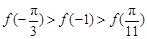 | B.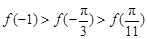 |
C. | D. |
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
 |  | 0 | 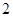 |  | 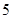 |
 |  | 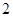 |  | 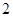 |  |

下列关于函数
 的命题:
的命题:①函数
 在
在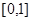 上是减函数;②如果当
上是减函数;②如果当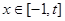 时,
时, 最大值是
最大值是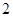 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为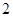 。
。其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
函数 的零点所在的区间为( )
的零点所在的区间为( )
A. | B. | C. | D. |
下列函数中,不满足 的是( )
的是( )
A.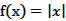 | B. | C. | D. |
设 ,若
,若 ,则
,则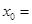 ( )
( )
A. | B. | C. | D. |
设 ,
, ,
, ,则
,则 的大小顺序是( )
的大小顺序是( )
A. | B. | C. | D.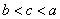 |
 的图象大致是
的图象大致是