题目内容
10.若集合A={x|x2+x-6=0},B={x|x2+x+a=0},且B⊆A,求实数a的取值范围.分析 求解一元二次方程化简A,然后分B为∅,单元素集合,双元素集合求得满足B⊆A的实数a的取值范围.
解答 解:A={x|x2+x-6=0}={-3,2},B={x|x2+x+a=0},
当1-4a<0,即$a>\frac{1}{4}$时,B=∅,满足B⊆A;
当1-4a=0,即a=$\frac{1}{4}$时,方程x2+x+a=0化为x2+x+$\frac{1}{4}$=0,解得x=-$\frac{1}{2}$,B={-$\frac{1}{2}$},不满足B⊆A;
当1-4a>0,即a<$\frac{1}{4}$时,要使B⊆A,则-3,2应为方程x2+x+a=0的两不等根,
∴$\left\{\begin{array}{l}{-3+2=-1}\\{-3×2=a}\end{array}\right.$,即a=-6.
综上,实数a的取值范围是{-6}∪($\frac{1}{4},+∞$).
点评 本题考查子集与真子集,考查了分类讨论的数学思想方法,训练了利用判别式法分析方程的根,是中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
5.已知函数f(x)满足f(x)•f(x+2)=1,且f(1)=2,则f(99)=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 99 |
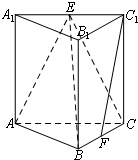 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1、BC的中点.