题目内容
(本小题满分13分)已知数列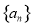 满足
满足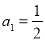 ,
, ,数列
,数列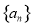 的前n项和为
的前n项和为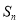 ,
,
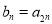 ,其中
,其中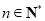 .
.
(1)求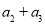 的值;
的值;
(2)证明:数列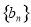 为等比数列;
为等比数列;
(3)是否存在 ,使得
,使得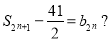 若存在,求出所有的n的值;若不存在,请说明理由.
若存在,求出所有的n的值;若不存在,请说明理由.
(1)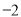 ;(2)详见解析;(3)存在唯一的
;(2)详见解析;(3)存在唯一的 ,使得
,使得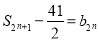 成立.
成立.
【解析】
试题分析:(1)由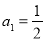 ,根据递推公式可求得
,根据递推公式可求得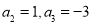 ,所以有
,所以有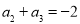 .
.
(2)由题设知: ,由此可证数列
,由此可证数列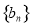 为等比数列;
为等比数列;
(3)由 (2)知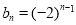 ,所以
,所以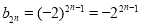 .
.
由于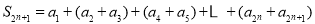 ,则令
,则令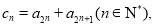 由题设中的递推公式易得:
由题设中的递推公式易得: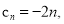 由此求出求出
由此求出求出 的表达式,将原问题转化为函数方程问题.
的表达式,将原问题转化为函数方程问题.
试题解析: 【解析】
(1)因为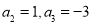 ,所以
,所以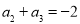 .
.
(或者根据已知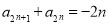 ,可得
,可得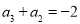 .) 3分
.) 3分
(2)证明: ,
,
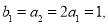 ,故数列
,故数列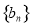 是首项为1,公比为-2的等比数列. 7分
是首项为1,公比为-2的等比数列. 7分
(3)由(2)知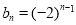 ,
,
所以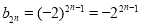 .
.
设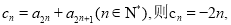 ,
,
又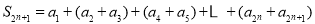
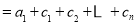
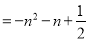 .
.
则由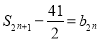 ,得
,得 ,
,
设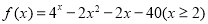 ,
,
则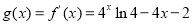 ,
,
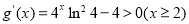 ,所以
,所以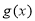 在
在 上单调递增,
上单调递增,
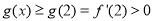 ,即
,即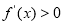 ,所以
,所以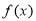 在
在 上单调递增
上单调递增
又因为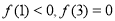 ,
,
所以仅存在唯一的 ,使得
,使得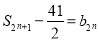 成立. 13分
成立. 13分
考点:1、数列的递推公式;2、等差数列与等比数列;3、用函数方程的思想解决数列问题.

练习册系列答案
相关题目
 中,底面
中,底面 是正方形,
是正方形,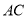 与
与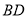 交于点
交于点 ,
,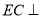 底面
底面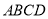 ,
, 为
为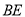 的中点.
的中点. 
 ∥平面
∥平面 ;
;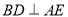 ;
;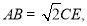 在线段
在线段 上是否存在点
上是否存在点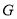 ,使
,使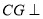 平面
平面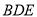 ?
? 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.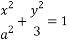 的右焦点为F,直线
的右焦点为F,直线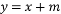 与椭圆E交于A,B两点.若△EAB周长的最大值是8,则m的值等于 ( ).
与椭圆E交于A,B两点.若△EAB周长的最大值是8,则m的值等于 ( ). D. 2
D. 2 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= . “
“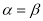 ”是“
”是“ ”的
”的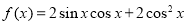 .
.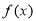 的最小正周期;
的最小正周期;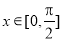 时,求函数
时,求函数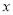 值.
值. 的单调递增区间是 .
的单调递增区间是 . 分别为
分别为 和椭圆
和椭圆 上的点,则
上的点,则