题目内容
(本小题满分13分)已知函数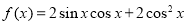 .
.
(1)求函数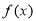 的最小正周期;
的最小正周期;
(2)当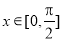 时,求函数
时,求函数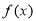 的最大值及取得最大值时的
的最大值及取得最大值时的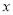 值.
值.
(1) ; (2)当
; (2)当 时,即
时,即 时,所以
时,所以 有最大值
有最大值 .
.
【解析】
试题分析:(1)首先利用三角函数二倍角公式及两角和与差的三角函数公式将函数 的解析式化成只含一个角的三角函数,然后利用正弦函数的性质求它的最小正周期;
的解析式化成只含一个角的三角函数,然后利用正弦函数的性质求它的最小正周期;
(2)由(1)得: ,利用
,利用 求出
求出 的范围,进而利用正弦函数的性质求出函数
的范围,进而利用正弦函数的性质求出函数 的最大值及取得最大值时的
的最大值及取得最大值时的 值.
值.
试题解析:【解析】
(Ⅰ)因为 

 5分
5分
所以  ,故
,故 的最小正周期为
的最小正周期为 . 7分
. 7分
(2)因为  , 所以
, 所以 . 9分
. 9分
当 时,即
时,即 时, 11分
时, 11分
所以 有最大值
有最大值 . 13分
. 13分
考点:1、三角函数的性质;2、三角函数的恒等变形.

练习册系列答案
相关题目

 与直线x=1,x=2及x轴围城的封闭图形的面积是( ) .
与直线x=1,x=2及x轴围城的封闭图形的面积是( ) . 满足
满足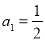 ,
, ,数列
,数列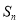 ,
,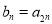 ,其中
,其中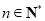 .
.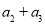 的值;
的值;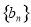 为等比数列;
为等比数列; ,使得
,使得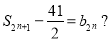 若存在,求出所有的n的值;若不存在,请说明理由.
若存在,求出所有的n的值;若不存在,请说明理由. 的展开式中,
的展开式中, 的系数是 .(用数字作答)
的系数是 .(用数字作答) 的值是
的值是
 B.
B. C.
C. D.
D.
 的解集为( )
的解集为( )  B.
B.
 D.
D.
 与曲线
与曲线 有四个不同交点,则实数
有四个不同交点,则实数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.