题目内容
5.若函数f(x)=x3-$\frac{3}{2}$ax2+a在R上存在三个零点,则实数a的取值范围是( )| A. | a>$\sqrt{2}$ | B. | a>$\sqrt{2}$或a<-$\sqrt{2}$ | C. | a<-$\sqrt{2}$ | D. | a<-1 |
分析 根据函数函数f(x)有三个相异的零点,可得函数f(x)的极大值与极小值异号,利用导数确定函数的极大值与极小值,从而可得不等式,故可求实数a的取值范围
解答 解:∵函数f(x)=)=x3-$\frac{3}{2}$ax2+a在x∈R上有三个零点,
∴函数f(x)的极大值与极小值异号.
∵f′(x)=3x2-3ax
∴f′(x)=0时,x=0或x=a
∴f(0)×f(a)=a(a3-$\frac{3}{2}$a3+a)<0,
∴1-$\frac{1}{2}{a}^{2}$<0,
∴a>$\sqrt{2}$,或a<$-\sqrt{2}$,
故选:B
点评 本题以函数为载体,考查函数的零点,考查利用导数求函数的极值,考查学生分析解决问题的能力,将函数f(x)有三个相异的零点,转化为函数f(x)的极大值与极小值异号是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知直线y=k(x-2)(k>0)与抛物线y2=8x相交于点A,B两点,F为抛物线的焦点,若|FA|=2|FB|,则k的值为( )
| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
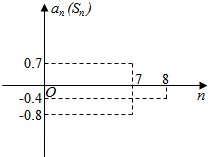 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.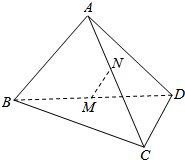 如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点.
如图,空间四边形ABCD各边边长均为a,M,N分别是对角线BD,AC的中点. 装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:
装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算: