Question

已知点A（-3，0）和圆O：x²+y²=9，AB是圆O的直径，M和N是AB的三等分点，P（异于A，B）是圆O上的动点，PD⊥AB于D，

PE

=λ

ED

(λ＞0)，直线PA与BE交于C，要使|CM|+|CN|为定值，则λ的值为（　　）

• A、

  1

  8

• B、

  1

  10

• C、

  1

  2

• D、1

Answer 1

考点：向量数乘的运算及其几何意义

专题：圆锥曲线的定义、性质与方程

分析：设P（m，n），则m²+n²=9，得到n²=9-m²．（*）设E（s，t），利用

PE

=λ

ED

（λ＞0），可得E(m，

n

1+λ

)．得到直线BE的方程为：y=

n 1+λ -0

m-3

(x-3)，又直线AP的方程为：y=

n-0

m+3

(x-3)．将两式相乘可得点C的轨迹方程，再利用椭圆的定义即可得出．

解答： 解：如图所示，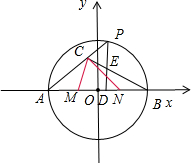
设P（m，n），则m²+n²=9，得到n²=9-m²．（*）
设E（s，t），∵

PE

=λ

ED

（λ＞0），
∴（s-m，t-n）=λ（0，-t），
解得

s=m t= n 1+λ

，
即E(m，

n

1+λ

)．
∴直线BE的方程为：y=

n 1+λ -0

m-3

(x-3)，
又直线AP的方程为：y=

n-0

m+3

(x-3)．
两式相乘可得：y2=

n2

(1+λ)(m2-9)

(x2-9)，
把（*）代入可得y2=

-1

1+λ

(x2-9)，即为点C的轨迹方程．
化为

x2

9

+

y2

9 1+λ

=1．
∵λ＞0，可知：点C在此椭圆上，焦点分别M（-1，0），N（1，0），a²=9．
∴1+

9

1+λ

=9，
解得λ=

1

8

．
因此当λ=

1

8

时，满足|CM|+|CN|=6为定值．
故λ=

1

8

．
故选：A．

点评：本题综合考查了圆的性质、椭圆的定义及其性质、直线相交问题，考查了分析问题和解决问题的能力，考查了计算能力，属于难题．