题目内容
已知函数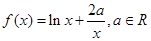 .
.
(1)若函数 在
在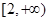 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若函数 在
在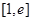 上的最小值为3,求实数
上的最小值为3,求实数 的值.
的值.
(1)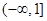 ;(2)
;(2)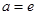 .
.
解析试题分析:(1)这是一个由函数在某区间上是增函数,求参数取值范围的问题,可转化为其导函数在此区间上恒大于或等于0的一个恒成立问题,恒成立问题是我们所熟悉的问题,可采用分离参数法进行解答,也可由函数本身的性质作出判断;(2)这是一个求含参函数在某区间上的最小值问题,可通过导数的符号去判断函数的单调区间,当然一般会涉及对参数的讨论,之后利用单调性则可求出函数的最小值,再由最小值为3,就可求出参数 的值.
的值.
(1)∵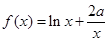 ,∴
,∴ 2分
2分
∵ 在
在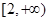 上是增函数
上是增函数
∴ ≥0在
≥0在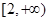 上恒成立,即
上恒成立,即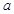 ≤
≤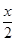 在
在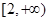 上恒成立 4分
上恒成立 4分
令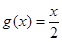 ,则
,则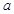 ≤
≤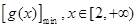
∵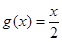 在
在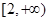 上是增函数,∴
上是增函数,∴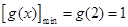
∴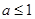 .所以实数
.所以实数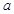 的取值范围为
的取值范围为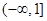 7分
7分
(2)由(1)得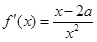 ,
,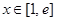
①若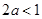 ,则
,则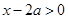 ,即
,即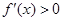 在
在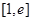 上恒成立,此时
上恒成立,此时 在
在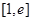 上是增函数
上是增函数
所以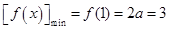 ,解得
,解得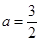 (舍去) 10分
(舍去) 10分
②若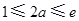 ,令
,令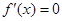 ,得
,得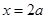 ,当
,当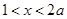 时,
时,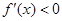 ,所以
,所以 在
在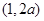 上是减函数,当
上是减函数,当 时,
时,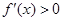 ,所以
,所以 在
在 上是增函数
上是增函数
所以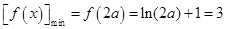 ,解得
,解得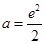 (舍去) 13分
(舍去) 13分
③若 ,则
,则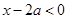 ,即
,即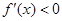 在
在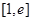 上恒成立,此时
上恒成立,此时 在
在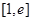 上是减函数
上是减函数
所以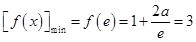 ,所以
,所以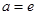 16分.
16分.
考点:1.函数的单调性与导数;2.函数的最值与导数;3.分类讨论的思想.

练习册系列答案
相关题目
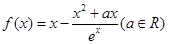 .
.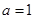 时,证明:当
时,证明:当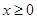 时,
时,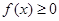 ;
;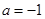 时,证明:
时,证明: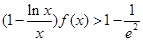 .
.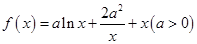 .若曲线
.若曲线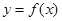 在点
在点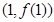 处的切线与直线
处的切线与直线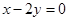 垂直,
垂直,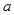 的值;
的值;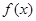 的单调区间;
的单调区间;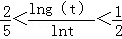 .
. 在点(1,0)处的切线.
在点(1,0)处的切线.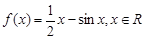 .
. 的递减区间;
的递减区间;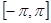 上的最值.
上的最值.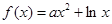 (
(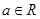 )
)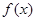 在区间[e,e2]上的最大值和最小值;
在区间[e,e2]上的最大值和最小值;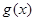 、
、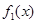 、
、 在公共定义域D上,满足
在公共定义域D上,满足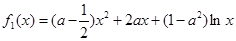 ,
,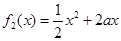 ,若在区间(1,+∞)上,函数
,若在区间(1,+∞)上,函数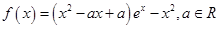 .
.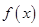 在
在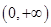 内单调递增,求
内单调递增,求 的取值范围;
的取值范围;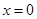 处取得极小值,求
处取得极小值,求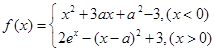 ,
,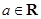 .
.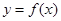 在
在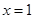 处取得极值,求
处取得极值,求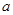 的值;
的值;