题目内容
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]() ,
, ![]() (或
(或![]() ,
, ![]() ;…)
;…)
【解析】试题分析:(1)将条件![]() 中分式变成整式得
中分式变成整式得![]() ,把
,把![]() 换成
换成![]() 得
得![]() ,两式相减化简可得
,两式相减化简可得![]() ,化简得
,化简得![]() ,根据等差数列定义可知数列
,根据等差数列定义可知数列![]() 为等差数列,由等差数列通项公式写出公式即可。(2)由(1)可得
为等差数列,由等差数列通项公式写出公式即可。(2)由(1)可得![]() ,因为数列
,因为数列![]() 是单调递增数列,所以
是单调递增数列,所以![]() ,
, ![]() ,化简得
,化简得![]() ,因为
,因为![]() 的正负与
的正负与![]() 是奇数、偶数有关,故分两种情况讨论。当
是奇数、偶数有关,故分两种情况讨论。当![]() 是奇数时,
是奇数时, ![]() 可变为
可变为![]() 恒成立,构造函数求不等式右边的最大值,令
恒成立,构造函数求不等式右边的最大值,令![]() ,用函数单调性定义可证明单调性为减函数,所以
,用函数单调性定义可证明单调性为减函数,所以![]() ;当
;当![]() 是偶数时,
是偶数时, ![]() 可变为
可变为![]() 恒成立,构造函数求不等式右边的最小值,令
恒成立,构造函数求不等式右边的最小值,令![]() ,利用函数单调性定义证明函数为增函数,所以
,利用函数单调性定义证明函数为增函数,所以![]() 。可得所求范围。(3)由(1)及
。可得所求范围。(3)由(1)及![]() 可求出
可求出![]() ,所以
,所以 ![]() 。假设对任意
。假设对任意![]() ,总存在正整数
,总存在正整数![]() ,使
,使![]() ,可得关于
,可得关于![]() 的关系式
的关系式 ![]() 整理可得
整理可得![]() ,给出
,给出![]() 的值,可求出
的值,可求出![]() 的值。
的值。
试题解析:解:(1) ![]()
![]()
∴![]() 是以
是以![]() 为首项,
为首项, ![]() 为公差的等差数列,∴
为公差的等差数列,∴![]()
(2) ![]() ,即
,即![]()
若![]() 为奇数,则
为奇数,则![]() 恒成立,
恒成立,
考察![]() ,
, 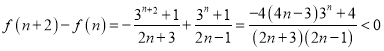
即![]() ,∴
,∴![]() ;
;
若![]() 为偶数,则
为偶数,则![]() 恒成立,
恒成立,
考察![]() ,
, 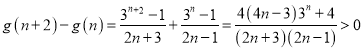
即![]() ,∴
,∴![]() ;综上所述,
;综上所述, ![]() ;
;
(3)由(1) ![]() .假设对任意
.假设对任意![]() ,总存在正整数
,总存在正整数![]() ,使
,使![]() ,
,
则![]()
令![]() ,则
,则![]() (或
(或![]() ,则
,则![]() ;…)
;…)
∴![]() (或
(或![]() ;…)
;…)

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目