题目内容
椭圆C经过点P(3,0),Q(0,-1)(Ⅰ)求椭圆C的标准方程,并求出椭圆C的长轴长、短轴长、离心率和焦点坐标.
(Ⅱ)设直线y=x+2交椭圆C于A,B两点,求线段AB的中点坐标.
分析:(Ⅰ)因为P(3,0),Q(0,-1)在坐标轴上,由椭圆标准方程定义易得a、b的值,进而求得椭圆C的长轴长、短轴长、离心率和焦点坐标
(Ⅱ)将直线与椭圆联立,运用韦达定理,设而不求的技巧,易得线段AB的中点坐标
(Ⅱ)将直线与椭圆联立,运用韦达定理,设而不求的技巧,易得线段AB的中点坐标
解答:解:(Ⅰ)由已知可得a=3,b=1,∴c=
=2
椭圆的标准方程为
+y2=1,
长轴长2a=6,短轴长 2b=2.
离心率e=
=
.
焦点为(2
,0),(-2
,0).
(Ⅱ)
得出10x2+36x+27=0
设A(x1,y1),B(x2,y2),线段AB的中点坐标为(x0,y0)
则x1+x2=-
,x0=
=-
,y0=x0+2=
∴线段AB的中点坐标为(-
,
)
| a2-b2 |
| 2 |
椭圆的标准方程为
| x2 |
| 9 |
长轴长2a=6,短轴长 2b=2.
离心率e=
| c |
| a |
2
| ||
| 3 |
焦点为(2
| 2 |
| 2 |
(Ⅱ)
|
设A(x1,y1),B(x2,y2),线段AB的中点坐标为(x0,y0)
则x1+x2=-
| 18 |
| 5 |
| x1+x2 |
| 2 |
| 9 |
| 5 |
| 1 |
| 5 |
| 9 |
| 5 |
| 1 |
| 5 |
点评:本题考查了椭圆标准方程的定义和求法,椭圆的几何意义,及直线与椭圆的关系,简单运用韦达定理,设而不求解决问题,属基础题

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
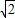 )且与x轴交于点F(2,0).
)且与x轴交于点F(2,0).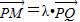 ,当
,当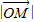 取最小值时,求λ的对应值.
取最小值时,求λ的对应值.