题目内容
3.函数$f(x)=\frac{2x}{x-1}(x≥3)$的最大值为3.分析 f(x)=$\frac{2x}{x-1}=\frac{2(x-1)+2}{x-1}=2+\frac{2}{x-1}$,易知函数f(x)在[3.+∞)上单调递减
解答 解:f(x)=$\frac{2x}{x-1}=\frac{2(x-1)+2}{x-1}=2+\frac{2}{x-1}$,易知函数f(x)在[3.+∞)上单调递减,所以x=3时函数$f(x)=\frac{2x}{x-1}(x≥3)$的最大值为3.
故答案为:3
点评 本题考查了求函数最值的基本方法,属于基础题.

练习册系列答案
相关题目
14.过抛物线y2=2px(p>0)的焦点F作两条相互垂直的射线,分别与抛物线相交于点M,N,过弦MN的中点P作抛物线准线的垂线PQ,垂足为Q,则$\frac{{|{PQ}|}}{{|{MN}|}}$的最大值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
18.执行如图所示的程序框图,输出的k值是( )


| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
8.新高考政策已经在上海和浙江试验实施.为了解学生科目选择的意向,从某校高一学生中随机抽取30位同学,对其选课情况进行统计分析,得到频率分布表如下:
(Ⅰ)若所抽取的30位同学中,有2位同学选择了“历史、地理、生物”组合,3位同学选择了“物理、政治、历史”组合.求a、b、c的值;
(Ⅱ)在(Ⅰ)的条件下,将选择了“历史、地理、生物”组合的2位同学记为x1、x2,选择了“物理、政治、历史”组合的3位同学记为y1、y2、y3.现从这5位同学中任取2位(假定每位同学被抽中的可能性相同),写出所有可能的结果,并求这两位同学科目选择恰好相同的概率.
| 科目选择 | 物理 化学 生物 | 历史 地理 政治 | 物理 化学 地理 | 历史 地理 生物 | 物理 政治 历史 | 其他 |
| 频率 | $\frac{1}{5}$ | $\frac{1}{6}$ | $\frac{2}{15}$ | a | b | c |
(Ⅱ)在(Ⅰ)的条件下,将选择了“历史、地理、生物”组合的2位同学记为x1、x2,选择了“物理、政治、历史”组合的3位同学记为y1、y2、y3.现从这5位同学中任取2位(假定每位同学被抽中的可能性相同),写出所有可能的结果,并求这两位同学科目选择恰好相同的概率.
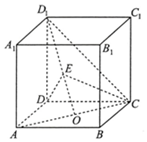 (理科)如图,在正方体ABCD-A1B1C1D1,O是AC的中点,E是线段D1O上一点,且$\frac{{D}_{1}E}{EO}$=λ.
(理科)如图,在正方体ABCD-A1B1C1D1,O是AC的中点,E是线段D1O上一点,且$\frac{{D}_{1}E}{EO}$=λ.