题目内容
13.函数f(x)=$\frac{\sqrt{1-co{s}^{2}x}}{cosx}$( )| A. | 在(-$\frac{π}{2}$,$\frac{π}{2}$)上递增 | B. | 在(-$\frac{π}{2}$,0]上递增,在(0,$\frac{π}{2}$)上递减 | ||
| C. | 在(-$\frac{π}{2}$,$\frac{π}{2}$)上递减 | D. | 在(-$\frac{π}{2}$,0]上递减,在(0,$\frac{π}{2}$)上递增 |
分析 f(x)=$\frac{\sqrt{1-co{s}^{2}x}}{cosx}$=$\frac{|sinx|}{cosx}$,去掉绝对值,即可得出结论.
解答 解:f(x)=$\frac{\sqrt{1-co{s}^{2}x}}{cosx}$=$\frac{|sinx|}{cosx}$,
在(-$\frac{π}{2}$,0]上,f(x)=-tanx,函数单调递减,在(0,$\frac{π}{2}$)上,f(x)=tanx,函数单调递增,
故选D.
点评 本题考查三角函数的性质,考查学生的转化能力,比较基础.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.已知集合A={-2,-1,0,1,2},B={x|$\frac{x+1}{x-2}$<0},则A∩B=( )
| A. | {0,1} | B. | {-1,0} | C. | {-1,0,1} | D. | {0,1,2} |
2.将函数f(x)=$\sqrt{3}$sinx+cosx的图象向右平移$\frac{π}{3}$后得到函数g(x)的图象,则函数g(x)的图象的一条对称轴方程是( )
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=-$\frac{π}{3}$ |
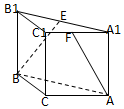 如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.
如图,ABC-A1B1C1是直三棱柱,∠BCA=90°,点E、F分别是A1B1、A1C1的中点,若BC=CA=AA1,则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$.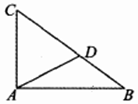 如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.
如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.