题目内容
证明:
+
+
+…+
<ln(n+1)<1+
+
+…+
.
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
考点:反证法与放缩法,不等式的证明
专题:不等式
分析:构造不等式x>ln(x+1),将1,
,
,…
分别代入,然后将同向不等式对应相加,化简即可证明右侧不等式.构造函数f(x)=ln(x+1)-ln(x)-
,通过判断函数的单调性以及函数的最值,然后利用累加法证明不等式即可.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 2 |
| 2x+1 |
解答:
解:∵函数f(x)=ex-x,由f′(x)=ex-1=0,得x=0,
当x∈(0,+∞)时,f′(x)>0,
∴f(x)在(0,+∞)上为增函数,
∴[f(x)]min=f(0)=1,
∴x∈R时,f(x)≥1,
当x>0时,ex>x+1,即x>ln(x+1),
则1>ln2,
>ln(
+1),…,
>ln(
+1),
1+
+
+…+
>ln2+ln
+ln
+…+ln
=ln(n+1),
∴ln(n+1)<1+
+
+…+
.
令f(x)=ln(x+1)-ln(x)-
,
求导,得 f'(x)=
-
+
=
-
=
=
<0
所以f(x)是单调减函数,而当x→+∞时,f(x)=ln(1+
)-
→0 所以f(x)>0,
对任意的x>0 由不等式ln(x+1)-lnx>
所以ln(n+1)-lnn>
,lnn-ln(n-1)>
,…ln3-ln2>
,ln2-ln1>
,
∴ln(n+1)-lnn+lnn-ln(n-1)+ln(n-1)-ln(n-2)+…+ln2-ln1>
+
+
+…+
,
即:
+
+
+…+
<ln(n+1),
∴
+
+
+…+
<ln(n+1)<1+
+
+…+
当x∈(0,+∞)时,f′(x)>0,
∴f(x)在(0,+∞)上为增函数,
∴[f(x)]min=f(0)=1,
∴x∈R时,f(x)≥1,
当x>0时,ex>x+1,即x>ln(x+1),
则1>ln2,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 4 |
| 3 |
| n+1 |
| n |
∴ln(n+1)<1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
令f(x)=ln(x+1)-ln(x)-
| 2 |
| 2x+1 |
求导,得 f'(x)=
| 1 |
| x+1 |
| 1 |
| x |
| 4 |
| (2x+1)2 |
| 4 |
| (2x+1)2 |
| 1 |
| x(x+1) |
| 4x(x+1)-(2x+1)2 |
| x(x+1)(2x+1)2 |
| -1 |
| x(x+1)(2x+1)2 |
所以f(x)是单调减函数,而当x→+∞时,f(x)=ln(1+
| 1 |
| x |
| 2 |
| 2x+1 |
对任意的x>0 由不等式ln(x+1)-lnx>
| 2 |
| 2x+1 |
所以ln(n+1)-lnn>
| 2 |
| 2n+1 |
| 2 |
| 2n-1 |
| 2 |
| 5 |
| 2 |
| 3 |
∴ln(n+1)-lnn+lnn-ln(n-1)+ln(n-1)-ln(n-2)+…+ln2-ln1>
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2n+1 |
即:
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2n+1 |
∴
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
点评:本题主要考查了不等式的证明,放缩法的应用,构造函数函数的最值的应用,以及利用同向不等式的加法证明不等式,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
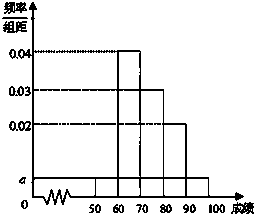 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 如图,设M点是圆C:x2+(y-4)2=4上的动点,过点M作圆O:x2+y2=1的两条切线,切点分别为A,B,切线MA,MB分别交x轴于D,E两点.
如图,设M点是圆C:x2+(y-4)2=4上的动点,过点M作圆O:x2+y2=1的两条切线,切点分别为A,B,切线MA,MB分别交x轴于D,E两点.