题目内容
13.判断函数y=tanx-sinx的奇偶性.分析 求出函数的定义域,结合函数奇偶性的定义进行判断.
解答 解:函数的定义域为{x|x≠kπ-$\frac{π}{2}$,k∈Z}定义域关于原点对称,
则f(-x)=tan(-x)-sin(-x)=-tanx+sinx=-(tanx-sinx)=-f(x),
则函数y=tanx-sinx为奇函数.
点评 本题主要考查函数奇偶性的判断,求出函数的定义域以及利用函数奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
8.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | f(x)=$\frac{1}{1+{x}^{2}}$ | B. | f(x)=x2+x | C. | f(x)=cos$\frac{x}{3}$ | D. | f(x)=$\frac{2}{x}$ |
3.在△ABC中,$\overrightarrow{AD}$=$2\overrightarrow{DB}$,若$\overrightarrow{CB}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,则$\overrightarrow{CD}$=( )
| A. | $\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$ | B. | $\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$ | C. | $\frac{3}{5}\overrightarrow{a}+\frac{4}{5}\overrightarrow{b}$ | D. | $\frac{4}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$ |
10.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )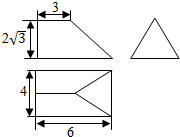

| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
7.函数f(x)=Asin(ωx+$\frac{π}{6}$)(A>0,ω>0)的图象与x轴的交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{2π}{3}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |