题目内容
函数f(x)=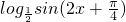 在[-
在[- ,
, ]上的单调减区间为________.
]上的单调减区间为________.
(- ,
, )
)
分析:首先根据对数的真数大于0,解不等式sin(2x+ )>0并结合x∈[-
)>0并结合x∈[- ,
, ],得到函数的定义域为(-
],得到函数的定义域为(- ,
, ).然后根据复合函数单调性法则可得函数在区间(-
).然后根据复合函数单调性法则可得函数在区间(- ,
, )是减函数,得到本题答案.
)是减函数,得到本题答案.
解答:函数的定义域满足{x|sin(2x+ )>0},
)>0},
即{x|2kπ<2x+ <2kπ+π,k∈Z},解之得{x|kπ-
<2kπ+π,k∈Z},解之得{x|kπ- <x<2kπ+
<x<2kπ+ ,k∈Z},
,k∈Z},
∵x∈[- ,
, ],
],
∴取k=0,得函数的定义域为(- ,
, )
)
∵0< <1,当x∈(-
<1,当x∈(- ,
, )时,t=sin(2x+
)时,t=sin(2x+ )是增函数.
)是增函数.
∴当x∈(- ,
, )时,y=
)时,y= 是减函数,
是减函数,
由此可得f(x)=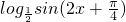 在[-
在[- ,
, ]上的单调减区间为(-
]上的单调减区间为(- ,
, )
)
故答案为:(- ,
, )
)
点评:本题给出含有三角函数的对数型函数,求函数在[- ,
, ]上的单调减区间.着重考查了三角函数的图象与性质、对数函数的单调性和复合函数单调性法则等知识,属于中档题.
]上的单调减区间.着重考查了三角函数的图象与性质、对数函数的单调性和复合函数单调性法则等知识,属于中档题.
 ,
, )
)分析:首先根据对数的真数大于0,解不等式sin(2x+
 )>0并结合x∈[-
)>0并结合x∈[- ,
, ],得到函数的定义域为(-
],得到函数的定义域为(- ,
, ).然后根据复合函数单调性法则可得函数在区间(-
).然后根据复合函数单调性法则可得函数在区间(- ,
, )是减函数,得到本题答案.
)是减函数,得到本题答案.解答:函数的定义域满足{x|sin(2x+
 )>0},
)>0},即{x|2kπ<2x+
 <2kπ+π,k∈Z},解之得{x|kπ-
<2kπ+π,k∈Z},解之得{x|kπ- <x<2kπ+
<x<2kπ+ ,k∈Z},
,k∈Z},∵x∈[-
 ,
, ],
],∴取k=0,得函数的定义域为(-
 ,
, )
)∵0<
 <1,当x∈(-
<1,当x∈(- ,
, )时,t=sin(2x+
)时,t=sin(2x+ )是增函数.
)是增函数.∴当x∈(-
 ,
, )时,y=
)时,y= 是减函数,
是减函数,由此可得f(x)=
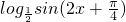 在[-
在[- ,
, ]上的单调减区间为(-
]上的单调减区间为(- ,
, )
)故答案为:(-
 ,
, )
)点评:本题给出含有三角函数的对数型函数,求函数在[-
 ,
, ]上的单调减区间.着重考查了三角函数的图象与性质、对数函数的单调性和复合函数单调性法则等知识,属于中档题.
]上的单调减区间.着重考查了三角函数的图象与性质、对数函数的单调性和复合函数单调性法则等知识,属于中档题. 
练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目