题目内容
(本小题共14分)
已知函数![]()
![]()
(I)若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(II)若![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围.
的取值范围.
(共14分)
解:(Ⅰ)因为![]() , …………………2分
, …………………2分
由![]() 即
即![]() 得
得![]() , …………………4分
, …………………4分
所以![]() 的解析式为
的解析式为![]() . …………………5分
. …………………5分
(Ⅱ)若![]() ,则
,则![]() ,
,![]() , …………………6分
, …………………6分
(1)当![]() ,即
,即![]() 时,
时,![]() 恒成立,那么
恒成立,那么![]() 在
在![]() 上单调递增,
上单调递增,
所以,当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增; …………………8分
上单调递增; …………………8分
(2)解法1:当![]() ,即
,即![]() 或
或![]() 时,
时,
令![]() 解得
解得![]() ,
,![]()
…………………9分
列表分析函数![]() 的单调性如下:
的单调性如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…………………10分
要使函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
只需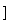 或
或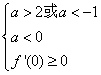 ,
,
解得![]() 或
或![]() . …………………13分
. …………………13分
解法2:当![]() ,即
,即![]() 或
或![]() 时,
时,
因为![]() 的对称轴方程为
的对称轴方程为![]() …………………9分
…………………9分
要使函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
需![]() 或
或![]()
解得![]() 或
或![]() . …………………13分
. …………………13分
综上:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增. …………………14分
上单调递增. …………………14分

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.