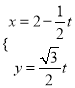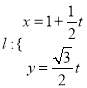题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(Ⅱ)若函数![]() 无零点,求
无零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)单调减区间为![]() 和
和![]() ;(Ⅱ)
;(Ⅱ) ![]() 的取值范围为:
的取值范围为: ![]() 或
或![]() .
.
【解析】试题分析:
(Ⅰ)利用切线求出参数![]() 值为2,解不等式
值为2,解不等式![]() 可得减区间;
可得减区间;
(Ⅱ)函数![]() 无零点,即方程
无零点,即方程![]() 在
在![]() 内无解,亦即要
内无解,亦即要![]() 在
在![]() 内无解.为此构造函数
内无解.为此构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性,可得结论,注意对
的单调性,可得结论,注意对![]() 分类讨论
分类讨论
试题解析:
(Ⅰ)解:![]() ,
,
又由题意有:![]()
![]() ,故
,故![]() .
.
此时,![]() ,由
,由![]() 或
或![]() ,
,
所以函数![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
(Ⅱ)解:
![]()
![]() ,且定义域为
,且定义域为![]() ,
,
要函数![]() 无零点,即要
无零点,即要![]() 在
在![]() 内无解,
内无解,
亦即要![]() 在
在![]() 内无解.
内无解.
构造函数![]() .
.
①当![]() 时,
时,![]() 在
在![]() 内恒成立,所以函数
内恒成立,所以函数![]() 在
在![]() 内单调递减,
内单调递减,![]() 在
在![]() 内也单调递减.又
内也单调递减.又![]() ,所以在
,所以在![]() 内无零点,
内无零点,
在![]() 内也无零点,故满足条件;
内也无零点,故满足条件;
②当![]() 时,
时,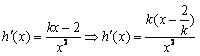
⑴若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内也单调递减,在
内也单调递减,在![]() 内单调递增.又
内单调递增.又![]() ,所以在
,所以在![]() 内无零点;易知
内无零点;易知![]() ,而
,而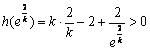 ,故在
,故在![]() 内有一个零点,所以不满足条件;
内有一个零点,所以不满足条件;
⑵若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.又
内单调递增.又![]() ,所以
,所以![]() 时,
时,![]() 恒成立,故无零点,满足条件;
恒成立,故无零点,满足条件;
⑶若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,在
内单调递增,在![]() 内也单调递增.又
内也单调递增.又![]() ,所以在
,所以在![]() 及
及![]() 内均无零点.
内均无零点.
又易知![]() ,而
,而![]() ,又易证当
,又易证当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 内有一零点,故不满足条件.
内有一零点,故不满足条件.
综上可得:![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目