题目内容
已知函数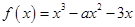
(1)若 在
在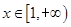 上是增函数,求实数
上是增函数,求实数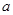 的取值范围;
的取值范围;
(2)若 是
是 的极值点,求
的极值点,求 在
在 上的最小值和最大值.
上的最小值和最大值.
(1)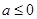 (2)f(x)max=f(1)=-6,f(x)min=-18.
(2)f(x)max=f(1)=-6,f(x)min=-18.
解析试题分析:(1)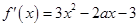 .
.
所以,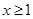 时,
时, 恒成立,即
恒成立,即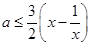 恒成立 3分
恒成立 3分
记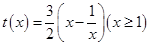 ,
,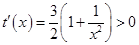
当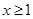 时,t(x)是增函数,∴
时,t(x)是增函数,∴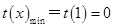 5分
5分
故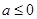 . 6分
. 6分
(2)由题意,得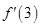 =0,即27-6a-3=0,∴a=4, 7分
=0,即27-6a-3=0,∴a=4, 7分
∴f(x)=x3-4x2-3x,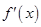 =3x2-8x-3.
=3x2-8x-3.
令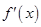 =0,得x1=-
=0,得x1=- ,x2=3. 8分
,x2=3. 8分
当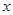 变化时,
变化时,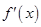 、
、 的变化情况如下表:
的变化情况如下表:
∴当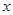
1 (1,3) 3 (3,4) 4 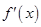
- 0 + 
-6 
极小值 
-12 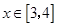 时,
时, 是增函数;当
是增函数;当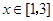 时,
时, 是减函数.
是减函数.
于是, 有极小值f(3)=-18; 10分
有极小值f(3)=-18; 10分
而f(1)=-6,f(4)=-12,
∴f(x)max=f(1)=-6,f(x)min=-18. 12分
考点:导数的运用
点评:解决的关键是利用导数的符号判定函数单调性,以及求解函数的极值和最值,属于基础题。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
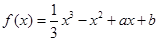 的图像在点
的图像在点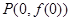 处的切线方程为
处的切线方程为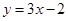 .
.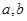 的值;
的值;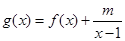 是[
是[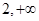 )上的增函数, 求实数
)上的增函数, 求实数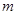 的最大值.
的最大值.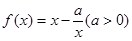 ,
,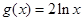 ,
,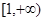 内的一切实数
内的一切实数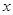 ,不等式
,不等式 恒成立,求实数
恒成立,求实数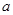 的取值范围;
的取值范围;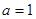 时,求最大的正整数
时,求最大的正整数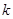 ,使得对
,使得对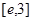 (
(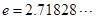 是自然对数的底数)内的任意
是自然对数的底数)内的任意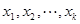 都有
都有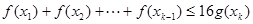 成立;
成立;
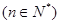 .
.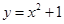 ,直线
,直线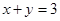 以及两坐标轴所围成的图形的面积S.
以及两坐标轴所围成的图形的面积S.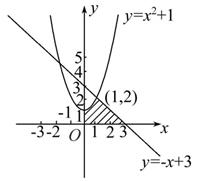
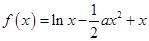 ,
,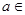 R.
R.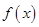 的单调区间;
的单调区间;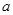 ,使得函数
,使得函数 ?若存在,求
?若存在,求 +
+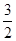 x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.(1)求a的值;(2)求函数f(x)的极值.
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.(1)求a的值;(2)求函数f(x)的极值.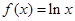 ,
,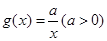 ,设
,设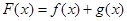 .
.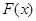 的单调区间;
的单调区间;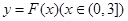 图像上任意一点
图像上任意一点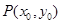 为切点的切线的斜率
为切点的切线的斜率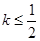 恒成立,求实数
恒成立,求实数 的最小值;
的最小值;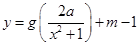 的图像与函数
的图像与函数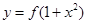 的图像恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由。
的图像恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由。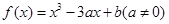 .
.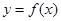 在点
在点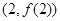 处与直线
处与直线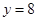 相切,求
相切,求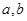 的值;
的值;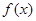 的极值点与极值.
的极值点与极值.