题目内容
(本小题满分12分)
设函数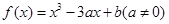 .
.
(Ⅰ)若曲线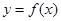 在点
在点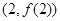 处与直线
处与直线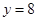 相切,求
相切,求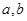 的值;
的值;
(Ⅱ)求函数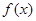 的极值点与极值.
的极值点与极值.
(Ⅰ) (Ⅱ)
(Ⅱ) 是
是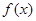 的极大值点,
的极大值点, 是
是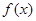 的极小值点.
的极小值点.
解析试题分析:(Ⅰ) ,∵曲线
,∵曲线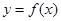 在点
在点 处与直线
处与直线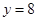 相切,
相切,
∴
(Ⅱ)∵ ,
,
当 时,
时, ,函数
,函数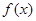 在
在 上单调递增,此时函数
上单调递增,此时函数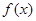 没有极值点.
没有极值点.
当 时,由
时,由 ,
,
当 时,
时, ,函数
,函数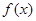 单调递增,
单调递增,
当 时,
时, ,函数
,函数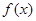 单调递减,
单调递减,
当 时,
时, ,函数
,函数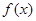 单调递增,
单调递增,
∴此时 是
是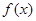 的极大值点,
的极大值点, 是
是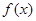 的极小值点.
的极小值点.
极值
考点:函数导数的几何意义及导数求极值
点评:函数导数的几何意义:函数在某点处的导数值等于该点处的切线斜率,函数的极值点处导数为零

练习册系列答案
相关题目
 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围; 是
是 上的最小值和最大值.
上的最小值和最大值.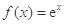 (
(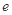 为自然对数的底数),
为自然对数的底数),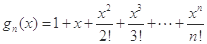 (
( ).
).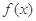
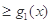 ;
;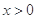 时,比较
时,比较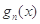 的大小,并说明理由;
的大小,并说明理由;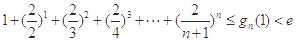 (
( ,
, 的单调区间和极值点;
的单调区间和极值点; ,记过点
,记过点 与原点的直线斜率为
与原点的直线斜率为 。是否存在
。是否存在 使
使 ?若存在,求出
?若存在,求出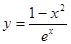 , 求
, 求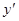
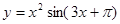 , 求
, 求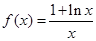 。
。 如果
如果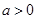 ,函数在区间
,函数在区间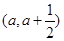 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围; 当
当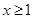 时,不等式
时,不等式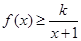 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。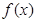 =
= (
( 为自然对数的底数),
为自然对数的底数), ,记
,记 .
. 为
为 的导函数,判断函数
的导函数,判断函数 的单调性,并加以证明;
的单调性,并加以证明; =0有两个零点,求实数
=0有两个零点,求实数 的取值范围.
的取值范围. .
. 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围; .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围. 在
在 及
及 时取得极值.
时取得极值. 的值;
的值; ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.