题目内容
11．某校安排5个班到4个工厂进行社会实践，每个班去一个工厂，每个工厂至少安排一个班，不同的安排方法共有240种．（用数字作答）分析 根据题意，分2步进行分析：先在5个班中任取2个班，即可将5个班级分成4组，再将分好的4组全排列，对应到4个工厂，由分步计数原理计算可得答案．
解答 解：根据题意，安排5个班到4个工厂进行社会实践，每个班去一个工厂，每个工厂至少安排一个班，需要有2个班去同一个工厂，
分2步进行分析：
①、将5个班级分成4组，其中一组有2个班级，有C52=10种分组方法，
②、将分好的4组全排列，对应到4个工厂，有A44=24种情况，
则不同的安排方法共有10×24=240种；
故答案为：240．
点评 本题考查排列、组合的综合应用，注意要先分好组，再进行排列，对应到工厂．
练习册系列答案
名校课堂系列答案
相关题目
1．如图所示，在△ABC中，BD=2CD，若$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，则$\overrightarrow{AD}$=（ ）
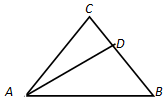
| A． | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B． | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C． | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D． | $\frac{2}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |
16．已知随机变量ξ～B（10，0.6），则E（ξ），D（ξ）分别是（ ）
| A． | 6和2.4 | B． | 4和2.4 | C． | 4和3.6 | D． | 6和1.6 |
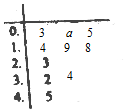已知函数f（x）=x2+$\sqrt{2}$（m-1）x+$\frac{m}{4}$，现有一组数据（该组数据数量庞大），从中随机抽取10个，绘制所得的茎叶图如图所示，且茎叶图中的数据的平均数为2．