题目内容
已知点P是函数y=lnx的图象上一点,在点P处的切线为l1,l1交x轴于点M,过点P作l1的垂线l2,l2交x轴于点N,MN的中点为Q,则点Q的横坐标的最大值为 .
考点:对数函数的图像与性质
专题:导数的综合应用
分析:设切点为(a,b),利用导数求出直线PM的方程,继而求出M点的横坐标,再根据直线PM⊥直线PN,求出直线PN的方程,继而求出N点的横坐标,根据中点坐标公式,求出Q点的横坐标,再利用导数求出最值,问题得以解决.
解答:
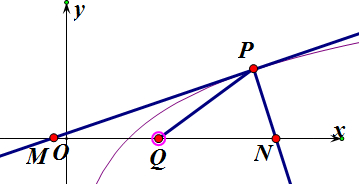 解:设P点的坐标为(a,b),如图所示,
解:设P点的坐标为(a,b),如图所示,
∵f(x)=lnx,
∴f′(x)=
,
∴直线PM的斜率kPM=f′(a)=
,
∴直线PM的方程为y-b=
(x-a),
令y=0,解得xM=a-ab,
∵直线PM⊥直线PN,
∴kPN=-
=-a,
直线PN的方程为y-b=-a(x-a),
令y=0,解得xN=a+
,
∵MN的中点为Q,
∴xQ=
(xM+xN=)=
( a-ab+a+
),
又b=lna,
∴xQ=
(a-alna+a+
),
令g(a)=a-alna+a+
,
∴g′(a)=1-(lna+1)+1+
=(1-lna)(1+
),
令g′(a)=0,解的a=e,
当0<a<e时,g′(a)>0,g(a)单调递增;
当a>e时,g'(a)<0,g(a)单调递减,
当a=e时取得极大值,即为最大值,最大值为g(e)=e-e+e+
=
,
故点Q的横坐标的最大值为
故答案为:
 解:设P点的坐标为(a,b),如图所示,
解:设P点的坐标为(a,b),如图所示,∵f(x)=lnx,
∴f′(x)=
| 1 |
| x |
∴直线PM的斜率kPM=f′(a)=
| 1 |
| a |
∴直线PM的方程为y-b=
| 1 |
| a |
令y=0,解得xM=a-ab,
∵直线PM⊥直线PN,
∴kPN=-
| 1 |
| kPM |
直线PN的方程为y-b=-a(x-a),
令y=0,解得xN=a+
| b |
| a |
∵MN的中点为Q,
∴xQ=
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| a |
又b=lna,
∴xQ=
| 1 |
| 2 |
| lna |
| a |
令g(a)=a-alna+a+
| lna |
| a |
∴g′(a)=1-(lna+1)+1+
| 1-lna |
| a2 |
| 1 |
| a2 |
令g′(a)=0,解的a=e,
当0<a<e时,g′(a)>0,g(a)单调递增;
当a>e时,g'(a)<0,g(a)单调递减,
当a=e时取得极大值,即为最大值,最大值为g(e)=e-e+e+
| 1 |
| e |
| e2+1 |
| e |
故点Q的横坐标的最大值为
| e2+1 |
| 2e |
故答案为:
| e2+1 |
| 2e |
点评:本题主要考查了曲线的切线方程和导数与最值得关系,关键是把点的坐标问题转化为求函数的最值问题,培养了学生的转化能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合M={x|x=
,k∈Z},集合N={x|x=
,k∈Z},则( )
| k |
| 4 |
| k |
| 8 |
| A、M∩N=∅ | B、M⊆N |
| C、N⊆M | D、M∪N=N |
-315°化为弧度是( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
有一串彩旗,▼代表蓝色,▽代表黄色.两种彩旗排成一行:
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有( )个黄旗.
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有( )个黄旗.
| A、111 | B、89 |
| C、133 | D、67 |
设Sn是等差数列{an}的前n项和,若a5=10a3,则
的值为( )
| S9 |
| S5 |
A、
| ||
| B、18 | ||
| C、1 | ||
D、
|