题目内容
【题目】已知函数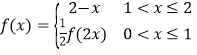 ,如果函数
,如果函数![]() 恰有三个不同的零点,那么实数
恰有三个不同的零点,那么实数![]() 的取值范围是________
的取值范围是________
【答案】![]()
【解析】
先求出函数的解析式,作出函数的图像,由题得![]() 有三个不同的实根,数形结合分析得到实数k的取值范围.
有三个不同的实根,数形结合分析得到实数k的取值范围.
当1<x≤2时,f(x)=-x+2,
当![]() 时,1<2x≤2,所以f(x)=
时,1<2x≤2,所以f(x)=![]() ,
,
当![]() 时,
时,![]() <2x≤1,所以f(x)=
<2x≤1,所以f(x)=![]() ,
,
当![]() 时,
时,![]() <2x≤
<2x≤![]() ,所以f(x)=
,所以f(x)=![]() ,
,
当![]() 时,
时,![]() <2x≤
<2x≤![]() ,所以f(x)=
,所以f(x)=![]() ,
,
![]()
所以函数的图像为:

其图像为线段PA,EB,GC,HD,![]() ,(不包括上端点A,B,C,D,
,(不包括上端点A,B,C,D,![]() )
)
直线y=k(x-1)表示过定点P(1,0)的直线系,
由题得C(![]() ),D(
),D(![]() ),
),
当直线在PD(可以取到)和直线PC(不能取到)之间时,直线和函数f(x)的图像有三个不同的交点,
由题得 .
.
所以k的取值范围为![]() .
.
故答案为:![]()

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】下表是某校120名学生假期阅读时间(单位: 小时)的频率分布表,现用分层抽样的方法从![]() ,
,![]() ,
,![]() ,
,![]() 四组中抽取20名学生了解其阅读内容,那么从这四组中依次抽取的人数是( )
四组中抽取20名学生了解其阅读内容,那么从这四组中依次抽取的人数是( )
分组 | 频数 | 频率 |
| 12 | 0.10 |
| 30 |
|
|
| 0.40 |
| n | 0.25 |
合计 | 120 | 1.00 |
A.2,5,8,5B.2,5,9,4C.4,10,4,2D.4,10,3,3





