题目内容
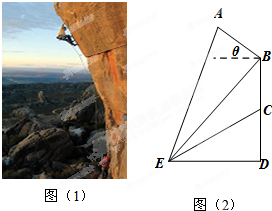 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,画出示意图,如图(2)所示,点A,C分别为两名攀岩者所在位置,点B为山的拐角处,且斜坡AB的坡角为θ,点D为山脚,某人在地面上的点E处测得A,B,C的仰角分别为α,β,γ,ED=a,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,画出示意图,如图(2)所示,点A,C分别为两名攀岩者所在位置,点B为山的拐角处,且斜坡AB的坡角为θ,点D为山脚,某人在地面上的点E处测得A,B,C的仰角分别为α,β,γ,ED=a,求:(Ⅰ)点B,D间的距离及点C,D间的距离;
(Ⅱ)在点A处攀岩者距地面的距离h.
分析:(I)分别在Rt△CDE和Rt△BED中利用正切在直角三角形的定义,可得CD=atanγ且BD=atanβ,即得所求距离.
(II)过A作AH⊥ED于H,则Rt△AEH中算出AE=
,同理BE=
,最后在三角形ABE中利用正弦定理,可算出点A处攀岩者距地面的距离h.
(II)过A作AH⊥ED于H,则Rt△AEH中算出AE=
| h |
| sinα |
| a |
| cosβ |
解答:解:(I)根据题意,得∠CED=γ,∠ABE=β,∠ADE=α
在Rt△CDE中,tanγ=
,得CD=atanγ
在Rt△BED中,tanβ=
,得BD=atanβ
综上所述,得点B,D间的距离为atanγ;点C,D间的距离为atanβ;
(II)过A作AH⊥ED于H,则
Rt△AEH中,AH=h,得sinα=
,所以AE=
,
同理,可得BE=
在△ABE中,∠AEB=α-β,∠EAB=π-(α+θ)
由正弦定理,得
=
,即AE=
=
∴h=AEsinα=

在Rt△CDE中,tanγ=
| CD |
| DE |
在Rt△BED中,tanβ=
| BD |
| DE |
综上所述,得点B,D间的距离为atanγ;点C,D间的距离为atanβ;
(II)过A作AH⊥ED于H,则
Rt△AEH中,AH=h,得sinα=
| h |
| AE |
| h |
| sinα |
同理,可得BE=
| a |
| cosβ |
在△ABE中,∠AEB=α-β,∠EAB=π-(α+θ)
由正弦定理,得
| BE |
| sin∠EAB |
| AE |
| sin∠ABE |
| BEsin(θ+β) |
| sin(α+θ) |
| asin(θ+β) |
| cosβsin(α+θ) |
∴h=AEsinα=
| asinαsin(θ+β) |
| cosβsin(α+θ) |
点评:本题给出实际问题,求点与点之间的距离并求攀岩处距离地面的距离,着重考查了直角三角形三角函数的定义和利用正弦定理解三角形的应用等知识,属于中档题.

练习册系列答案
相关题目
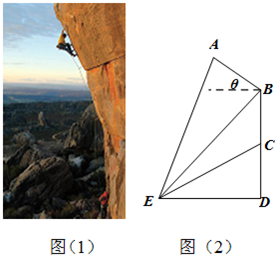 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
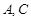 分别为两名攀岩者所在位置,点
分别为两名攀岩者所在位置,点 为山的拐角处,且斜坡AB的坡角为
为山的拐角处,且斜坡AB的坡角为 ,点
,点 为山脚,某人在地面上的点
为山脚,某人在地面上的点 处测得
处测得 的仰角分别为
的仰角分别为 ,
,
 ,
,
 间的距离及点
间的距离及点 间的距离;
间的距离; 处攀岩者距地面的距离
处攀岩者距地面的距离 .
.