题目内容
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E、F分别是AB、BD的中点,求证:
(1)直线EF∥平面ACD;
(2)平面EFC⊥平面BCD.
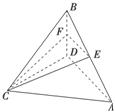
证明:(1)在△ABD中,因为E、F分别是AB、BD的中点,
所以EF∥AD.
又AD⊂平面ACD ,EF⊄平面ACD,
,EF⊄平面ACD,
所以直线EF∥平面ACD.
(2)在△ABD中,
因为AD⊥BD,EF∥AD,所以EF⊥BD.
在△BCD中,因为CD=CB,F为BD的中点,
所以CF⊥BD.
因为EF⊂平面EFC,CF⊂平面EFC,
EF与CF交于点F,所以BD⊥平面EFC.
又因为BD⊂平面BCD,所以平面EFC⊥平面BCD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某个体服装店经营某种服装,一周内获纯利y(元)与该周每天销售这种服装的件数x之间的一组数据如下:
| x | 3[ | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81[ | 89 | 90 | 91 |
已知: x
x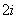 =280,
=280,
 y
y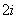 =45309,
=45309, xiyi=3487,此时r0.05=0.754.
xiyi=3487,此时r0.05=0.754.
(1)求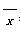 ,
,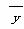 ;
;
(2)判断纯利润y与每天销售件数x之间是否线性相关.
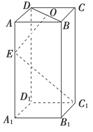
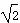 ,OE⊥EC1,求AA1的长
,OE⊥EC1,求AA1的长 .
.
 B.共面
B.共面 ,则cos〈
,则cos〈 的值为( )
的值为( )
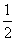 C.
C. D.
D.