Question

7．与圆x²+y²+6x+5=0外切，同时与圆x²+y²-6x-55=0内切，求动圆圆心的轨迹方程，并说明它是什么样的曲线？

Answer 1

分析 化两圆的一般方程为标准方程，求出圆心和半径，画出图形，由图可知动圆圆心的轨迹是以E、F为焦点，长轴长为10的椭圆（除去左顶点），则动圆圆心的轨迹方程可求．

解答 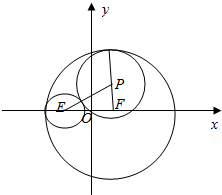解：由x²+y²+6x+5=0，得（x+3）²+y²=4，
∴圆心E（-3，0），半径为2，
由x²+y²-6x-55=0，得（x-3）²+y²=64，
∴圆心F（3，0），半径为8，
设动圆圆心为P（x，y），半径为r，
由动圆与圆x²+y²+6x+5=0外切，同时与圆x²+y²-6x-55=0内切，如图，
可得：|PE|+|PF|=r+2+8-r=10＞6，
∴动圆圆心的轨迹是以E、F为焦点，长轴长为10的椭圆（除去左顶点），
由a=5，c=3，得b²=a²-c²=25-9=16．
∴方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$（x≠-5）．

点评 本题考查圆与圆的位置关系的应用，考查了椭圆的定义及其标准方程的求法，考查数学转化思想方法，是中档题．