题目内容
本题有3小题,第1小题5分,第2小题5分,第3小题9分.
已知定义在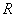 上的函数
上的函数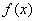 和数列
和数列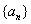 满足下列条件:
满足下列条件:
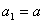 ,
,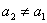 ,当
,当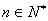 且
且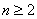 时,
时,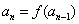 且
且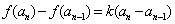 .
.
其中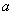 、
、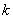 均为非零常数.
均为非零常数.
(1)若数列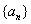 是等差数列,求
是等差数列,求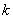 的值;
的值;
(2)令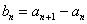
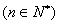 ,若
,若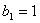 ,求数列
,求数列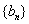 的通项公式;
的通项公式;
(3)试研究数列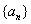 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.
说明:对于第3小题,将根据写出的条件所体现的对问题探究的完整性,给予不同的评分。
(1)由已知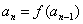 ,
,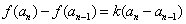
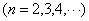 ,得
,得
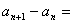
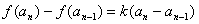
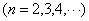
由数列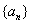 是等差数列,得
是等差数列,得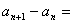
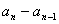
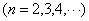
所以,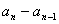
 ,
,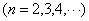 ,得
,得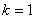 .………………………5分
.………………………5分
(2)由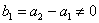 ,可得
,可得
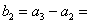
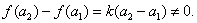
且当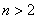 时,
时,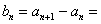
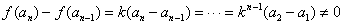
所以,当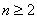 时,
时,
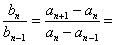
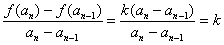 ,………………………4分
,………………………4分
因此,数列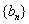 是一个公比为
是一个公比为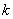 的等比数列.…………………………………………1分
的等比数列.…………………………………………1分
(3)解答一:写出必要条件,如,由(1)知,当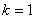 时,数列
时,数列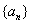 是等差数列,
是等差数列,
所以 是数列
是数列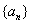 为等比数列的必要条件.
………………………………3分
为等比数列的必要条件.
………………………………3分
解答二:写出充分条件,如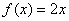 或
或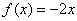 等,并证明 ……………… 5分
等,并证明 ……………… 5分
解答三: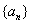 是等比数列的充要条件是
是等比数列的充要条件是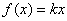
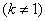 ……………………2分
……………………2分
充分性证明:
若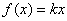
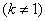 ,则由已知
,则由已知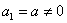 ,
,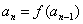
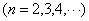 得
得
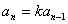
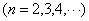
所以,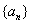 是等比数列.……………………………………………………………2分
是等比数列.……………………………………………………………2分
必要性证明:若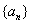 是等比数列,由(2)知,
是等比数列,由(2)知,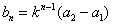
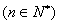
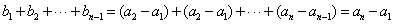
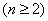 ,
,
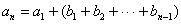 . …………………………………………1分
. …………………………………………1分
当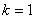 时,
时,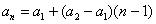
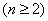 .
.
上式对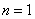 也成立,所以,数列
也成立,所以,数列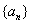 的通项公式为:
的通项公式为:
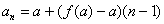
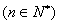 .
.
所以,当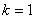 时,数列
时,数列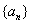 是以
是以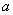 为首项,
为首项,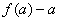 为公差的等差数列.
为公差的等差数列.
所以,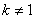 .……………………………………………………………………1分
.……………………………………………………………………1分
当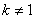 时,
时,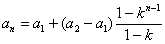
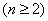 .
.
上式对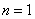 也成立,所以,
也成立,所以,
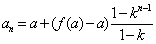
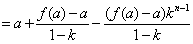 ……………………1分
……………………1分
所以,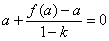
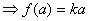 . …………………………………………1分
. …………………………………………1分
即,等式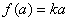 对于任意实数
对于任意实数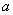 均成立.
均成立.
所以,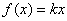
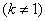 .……………………………………………………………1分
.……………………………………………………………1分

(本题满分13分)本题共有2个小题,第1小题满分5分,第2小题满分8分.
某校15名学生组成该校“科技创新周”志愿服务队(简称“科服队”),他们参加活动的有关数据统计如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人 数 | 3 | 4 | 8 |
(1)从“科服队”中任选3人,使得这3人参加活动次数各不相同,这样的选法共有多少种?
(2)从“科服队”中任选2人,求这2人参加活动次数之和大于3的概率.
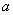 人.
人. 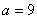 ,在计划时间内,该企业的人均年终奖是否会超过3万元?
,在计划时间内,该企业的人均年终奖是否会超过3万元?