题目内容
函数f(x)=(1)若P∩M=![]() ,则f(P)∩f(M)=
,则f(P)∩f(M)= ![]() ;
;
(2)若P∩M≠![]() ,则f(P)∩f(M)≠
,则f(P)∩f(M)≠![]() ;
;
(3)若P∪M=R,则f(P)∪f(M)=R;
(4)若P∪M≠R,则f(P)∪f(M)≠R.
其中正确的判断有( )
A.1个 B.2个 C.3个 D.4个
B
解析:若P={1,2},M={-1,-2},则P∩M=![]() .
.
但f(P)={1,2},f(M)={1,2},
所以f(P)∩f(M)={1,2},(1)不正确;
若P∩M≠![]() ,由函数的概念知,P、M有且只有一个公共元素0,
,由函数的概念知,P、M有且只有一个公共元素0,
所以f(P)与f(M)也至少有公共元素0,(2)正确;
若P={x|x≥0},M={x|x<0},P∪M=R,则f(P)={x|x≥0},f(M)={x|x>0},
所以f(P)∪f(M)≠R,(3)不正确;
若P∪M≠R,设x0![]() P且x0
P且x0![]() M,则x0
M,则x0![]() f(P)且-x0
f(P)且-x0![]() f(M),
f(M),
如果f(P)∪f(M)=R,则x0∈f(M)且-x0∈f(P),即-x0∈M且-x0∈P,由函数的概念知,x0=0.
而当0![]() (P∪M)时,必有0
(P∪M)时,必有0![]() f(P)∪f(M),(4)正确.
f(P)∪f(M),(4)正确.

练习册系列答案
相关题目
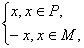 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=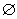 ,则f(P)∩f(M)=
,则f(P)∩f(M)=