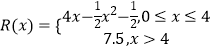题目内容
【题目】已知函数![]() ,函数
,函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
【答案】见解析
【解析】(1)因为![]() ,则由题意知
,则由题意知![]() ,所以
,所以![]() ,即
,即![]() .………1分
.………1分
所以![]() ,定义域为
,定义域为![]() .
.
![]() .……………2分
.……………2分
当![]() 时,由
时,由![]() ,得函数
,得函数![]() 的递增区间为
的递增区间为![]() ,
,
由![]() ,得函数
,得函数![]() 的递减区间为
的递减区间为![]() ;……………4分
;……………4分
当![]() 时,由
时,由![]() ,得函数
,得函数![]() 的递增区间为
的递增区间为![]() ,……………5分
,……………5分
(2)令![]() ,则
,则![]() .
.
根据题意,当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() .……………6分
.……………6分
①当![]() 时,
时,![]() ,
,![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符合题意. ……………7分
,所以不符合题意. ……………7分
②当![]() 时,
时,![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 所以不符合题意. ……………9分
所以不符合题意. ……………9分
③当![]() 时,
时,![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,
上是减函数,
于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,
,
即![]() ,解得
,解得![]() ,故取
,故取![]() ,……………11分
,……………11分
综上,![]() .……………12分
.……………12分
【命题意图】本题主要考查利用导数研究函数的单调性、函数与方程、不等式解法等基础知识,意在考查
逻辑推理能力、等价转化能力、运算求解能力,以及考查函数与方程思想、分类讨论思想.

练习册系列答案
相关题目