题目内容
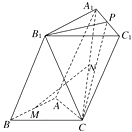
【题目】如图所示,四棱锥 ![]() 中,底面
中,底面 ![]() 为菱形,且直线
为菱形,且直线 ![]() 又棱
又棱 ![]()
![]() 为
为 ![]() 的中点,
的中点, ![]()

(Ⅰ) 求证:直线 ![]() ;
;
(Ⅱ) 求直线 ![]() 与平面
与平面 ![]() 的正切值.
的正切值.
【答案】解:证明:∵∠ADE=∠ABC=60°,ED=1,AD=2∴△AED是以∠AED为直角的Rt△
又∵AB∥CD, ∴EA⊥AB
又PA⊥平面ABCD,∴EA⊥PA,
∴EA⊥平面PAB,
(Ⅱ)
如图所示,连结PE,过A点作AH⊥PE于H点
∵CD⊥EA, CD⊥PA
∴CD⊥平面PAE,∴AH⊥CD,又AH⊥PE
∴AH⊥平面PCD
∴∠AEP为直线AE与平面PCD所成角
在Rt△PAE中,∵PA=2,AE= ![]()
∴ ![]()
【解析】(1)只需证明直线EA⊥AB,且EA⊥PA即可;
(2)先证明AH⊥平面PCD,得出∠AEP为直线AE与平面PCD所成角,在Rt△PAE中计算tan∠AEP的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目